Advertisements
Advertisements
प्रश्न
In an isosceles triangle PQR, the length of equal sides PQ and PR is 13 cm and base QR is 10 cm. Find the length of perpendicular bisector drawn from vertex P to side QR.
उत्तर

Given: In an isosceles triangle PQR, PQ = PR = 13 cm and base QR = 10 cm.
Since, PS is the perpendicular bisector,
∴ QS = SR = `(QR)/2 = 10/2` = 5
Now, using Pythagoras' theorem, in a right-angled triangle PSQ,
PS2 + SQ2 = PQ2
Substituting the values of SQ and PQ in equation (i),
PS2 + 52 = 132
⇒ PS2 = 132 – 52
⇒ PS2 = 169 – 25
⇒ PS2 = 144
∴ PS = `sqrt(144)` = 12
As a result, the length of the perpendicular bisector PS is 12 cm.
APPEARS IN
संबंधित प्रश्न
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
In Figure ABD is a triangle right angled at A and AC ⊥ BD. Show that AC2 = BC × DC

In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AD2 = BD × CD

PQR is a triangle right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

Diagonals of rhombus ABCD intersect each other at point O.
Prove that: OA2 + OC2 = 2AD2 - `"BD"^2/2`
In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
In the given figure, BL and CM are medians of a ∆ABC right-angled at A. Prove that 4 (BL2 + CM2) = 5 BC2.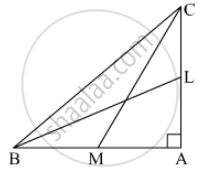
A ladder, 6.5 m long, rests against a vertical wall. If the foot of the ladder is 2.5 m from the foot of the wall, find up to how much height does the ladder reach?
In the figure below, find the value of 'x'.

Find the Pythagorean triplet from among the following set of numbers.
3, 4, 5
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = AE2 + CD2 + BF2
AD is perpendicular to the side BC of an equilateral ΔABC. Prove that 4AD2 = 3AB2.
In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
If ΔABC ~ ΔPQR, `("ar" triangle "ABC")/("ar" triangle "PQR") = 9/4` and AB = 18 cm, then the length of PQ is ______.
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
Points A and B are on the opposite edges of a pond as shown in figure. To find the distance between the two points, the surveyor makes a right-angled triangle as shown. Find the distance AB.

