Advertisements
Advertisements
प्रश्न
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
Advertisements
उत्तर
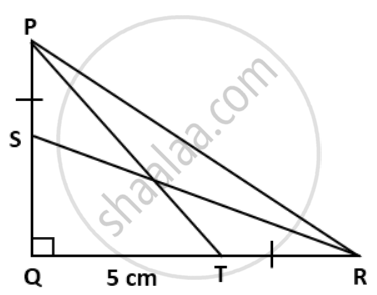
In ΔPQT, ∠Q = 90°
∴ PT2 = PQ2 + QT2 ....(By Pythagoras Theorem)
⇒ PQ2 = PT2 - QT2
⇒ PQ2 = PT2 - QT2
= 132 - 52
= 169 - 25
= 144
⇒ PQ = 12cm
Now, PS = TR = a (say)
In ΔSQR, ∠Q = 90°
∴ SR2 = QS2 + QR2 ....(By Pythagoras Theorem)
⇒ SR2 = (PQ - PS)2 + (QT + TR)2
⇒ SR2 = (PQ - PS)2 + (QT + PS)2
⇒ SR2 = PQ2 - 2 x PQ x PS + PS2 + QT2 + 2 x QT x PS + PS2
⇒ 132 = 122 - 2 x 12 x a + a2 + 52 + 2 x 5 x a + a2
⇒ 169 - 144 - 24a + a2 + 25 + 10a + a2
⇒ 169 = 169 - 14a + 2a2
⇒ 2a2 = 14a
⇒ a = 7
Hence, PS = 7cm.
APPEARS IN
संबंधित प्रश्न
If the sides of a triangle are 6 cm, 8 cm and 10 cm, respectively, then determine whether the triangle is a right angle triangle or not.
If ABC is an equilateral triangle of side a, prove that its altitude = ` \frac { \sqrt { 3 } }{ 2 } a`
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 7 cm, 24 cm, 25 cm
In Figure ABD is a triangle right angled at A and AC ⊥ BD. Show that AC2 = BC × DC
PQR is a triangle right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
In ∆ABC, AB = 10, AC = 7, BC = 9, then find the length of the median drawn from point C to side AB.
In the given figure, point T is in the interior of rectangle PQRS, Prove that, TS2 + TQ2 = TP2 + TR2 (As shown in the figure, draw seg AB || side SR and A-T-B)
In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
In the given figure, BL and CM are medians of a ∆ABC right-angled at A. Prove that 4 (BL2 + CM2) = 5 BC2.
In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.
Find the Pythagorean triplet from among the following set of numbers.
9, 40, 41
A ladder 25m long reaches a window of a building 20m above the ground. Determine the distance of the foot of the ladder from the building.
Each side of rhombus is 10cm. If one of its diagonals is 16cm, find the length of the other diagonals.
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9BP2 = 9BC2 + 4AC2
In the given figure, PQ = `"RS"/(3)` = 8cm, 3ST = 4QT = 48cm.
SHow that ∠RTP = 90°.
∆ABC is right-angled at C. If AC = 5 cm and BC = 12 cm. find the length of AB.
In figure, PQR is a right triangle right angled at Q and QS ⊥ PR. If PQ = 6 cm and PS = 4 cm, find QS, RS and QR.
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:
(i) `"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
(ii) `"AB"^2 = "AD"^2 - "BC"."DM" + (("BC")/2)^2`
(iii) `"AC"^2 + "AB"^2 = 2"AD"^2 + 1/2"BC"^2`
Two rectangles are congruent, if they have same ______ and ______.
