Advertisements
Advertisements
Question
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
Solution
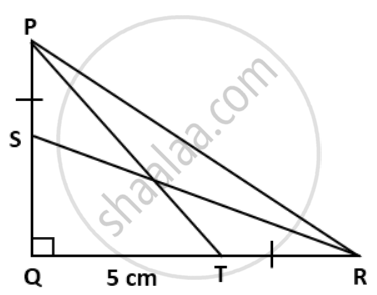
In ΔPQT, ∠Q = 90°
∴ PT2 = PQ2 + QT2 ....(By Pythagoras Theorem)
⇒ PQ2 = PT2 - QT2
⇒ PQ2 = PT2 - QT2
= 132 - 52
= 169 - 25
= 144
⇒ PQ = 12cm
Now, PS = TR = a (say)
In ΔSQR, ∠Q = 90°
∴ SR2 = QS2 + QR2 ....(By Pythagoras Theorem)
⇒ SR2 = (PQ - PS)2 + (QT + TR)2
⇒ SR2 = (PQ - PS)2 + (QT + PS)2
⇒ SR2 = PQ2 - 2 x PQ x PS + PS2 + QT2 + 2 x QT x PS + PS2
⇒ 132 = 122 - 2 x 12 x a + a2 + 52 + 2 x 5 x a + a2
⇒ 169 - 144 - 24a + a2 + 25 + 10a + a2
⇒ 169 = 169 - 14a + 2a2
⇒ 2a2 = 14a
⇒ a = 7
Hence, PS = 7cm.
APPEARS IN
RELATED QUESTIONS
The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
If ABC is an equilateral triangle of side a, prove that its altitude = ` \frac { \sqrt { 3 } }{ 2 } a`
In Figure ABD is a triangle right angled at A and AC ⊥ BD. Show that AC2 = BC × DC

In the following figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that

(i) OA2 + OB2 + OC2 − OD2 − OE2 − OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
In an equilateral triangle ABC, D is a point on side BC such that BD = `1/3BC` . Prove that 9 AD2 = 7 AB2
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
In the given figure, ∆ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices ?

Find the length diagonal of a rectangle whose length is 35 cm and breadth is 12 cm.
In the following figure, AD is perpendicular to BC and D divides BC in the ratio 1: 3.
Prove that : 2AC2 = 2AB2 + BC2
In the given figure, angle ACB = 90° = angle ACD. If AB = 10 m, BC = 6 cm and AD = 17 cm, find :
(i) AC
(ii) CD

In the right-angled ∆LMN, ∠M = 90°. If l(LM) = 12 cm and l(LN) = 20 cm, find the length of seg MN.
The sides of the triangle are given below. Find out which one is the right-angled triangle?
1.5, 1.6, 1.7
The length of the diagonals of rhombus are 24cm and 10cm. Find each side of the rhombus.
To get from point A to point B you must avoid walking through a pond. You must walk 34 m south and 41 m east. To the nearest meter, how many meters would be saved if it were possible to make a way through the pond?
Is the triangle with sides 25 cm, 5 cm and 24 cm a right triangle? Give reasons for your answer.
Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
