Advertisements
Advertisements
Question
In the right-angled ∆LMN, ∠M = 90°. If l(LM) = 12 cm and l(LN) = 20 cm, find the length of seg MN.
Solution
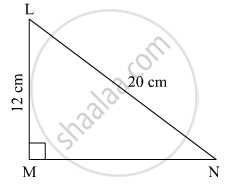
In the right-angled triangle LMN, ∠M = 90°. Hence, side LN is the hypotenuse.
According to Pythagoras' theorem,
l(LN)2 = l(MN)2 + l(LM)2
⇒ (20)2 = l(MN)2 + (12)2
⇒ 400 = l(MN)2 + 144
⇒ l(MN)2 = 400 − 144
⇒ l(MN)2 = 256
⇒ l(MN)2 = (16)2
⇒ l(MN) = 16
∴ Length of seg MN = 16 cm.
RELATED QUESTIONS
In the given figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2 = AB2 + BC2 − 2BC.BD.

A ladder, 6.5 m long, rests against a vertical wall. If the foot of the ladder is 2.5 m from the foot of the wall, find up to how much height does the ladder reach?
Find the Pythagorean triplet from among the following set of numbers.
4, 7, 8
A ladder 25m long reaches a window of a building 20m above the ground. Determine the distance of the foot of the ladder from the building.
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = AE2 + CD2 + BF2
Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
Choose the correct alternative:
If length of sides of a triangle are a, b, c and a2 + b2 = c2, then which type of triangle it is?
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
Points A and B are on the opposite edges of a pond as shown in figure. To find the distance between the two points, the surveyor makes a right-angled triangle as shown. Find the distance AB.

The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. Find the length of the ladder.
