Advertisements
Advertisements
प्रश्न
In the right-angled ∆LMN, ∠M = 90°. If l(LM) = 12 cm and l(LN) = 20 cm, find the length of seg MN.
उत्तर
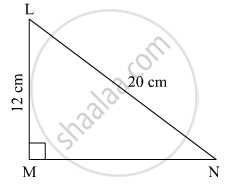
In the right-angled triangle LMN, ∠M = 90°. Hence, side LN is the hypotenuse.
According to Pythagoras' theorem,
l(LN)2 = l(MN)2 + l(LM)2
⇒ (20)2 = l(MN)2 + (12)2
⇒ 400 = l(MN)2 + 144
⇒ l(MN)2 = 400 − 144
⇒ l(MN)2 = 256
⇒ l(MN)2 = (16)2
⇒ l(MN) = 16
∴ Length of seg MN = 16 cm.
संबंधित प्रश्न
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Prove that, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the square of remaining two sides
Identify, with reason, if the following is a Pythagorean triplet.
(3, 5, 4)
A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.
In the figure, given below, AD ⊥ BC.
Prove that: c2 = a2 + b2 - 2ax.
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2) = (AB2 + PQ2)
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if: PQ = 34 cm and QR = 33.6 cm.
The sides of a certain triangle is given below. Find, which of them is right-triangle
16 cm, 20 cm, and 12 cm
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

