Advertisements
Advertisements
प्रश्न
The top of a ladder of length 15 m reaches a window 9 m above the ground. What is the distance between the base of the wall and that of the ladder?
उत्तर
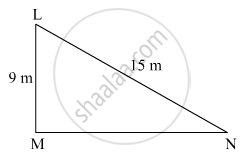
Let LN be the ladder of length 15 m that is resting against a wall. Let M be the base of the wall and L be the position of the window.
The window is 9 m above the ground. Now, MN is the distance between the base of the wall and that of the ladder.
In the right-angled triangle LMN, ∠M = 90°. Hence, side LN is the hypotenuse.
According to Pythagoras' theorem,
l(LN)2 = l(MN)2 + l(LM)2
⇒ (15)2 = l(MN)2 + (9)2
⇒ 225 = l(MN)2 + 81
⇒ l(MN)2 = 225 − 81
⇒ l(MN)2 = 144
⇒ l(MN)2 = (12)2
⇒ l(MN) = 12
∴ Length of seg MN = 12 m.
Hence, the distance between the base of the wall and that of the ladder is 12 m.
संबंधित प्रश्न
Identify, with reason, if the following is a Pythagorean triplet.
(10, 24, 27)
In the figure, given below, AD ⊥ BC.
Prove that: c2 = a2 + b2 - 2ax.
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
If the angles of a triangle are 30°, 60°, and 90°, then shown that the side opposite to 30° is half of the hypotenuse, and the side opposite to 60° is `sqrt(3)/2` times of the hypotenuse.
Choose the correct alternative:
In right-angled triangle PQR, if hypotenuse PR = 12 and PQ = 6, then what is the measure of ∠P?
Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
If ‘l‘ and ‘m’ are the legs and ‘n’ is the hypotenuse of a right angled triangle then, l2 = ________
Find the unknown side in the following triangles
Rithika buys an LED TV which has a 25 inches screen. If its height is 7 inches, how wide is the screen? Her TV cabinet is 20 inches wide. Will the TV fit into the cabinet? Give reason
Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
