Advertisements
Advertisements
Question
The top of a ladder of length 15 m reaches a window 9 m above the ground. What is the distance between the base of the wall and that of the ladder?
Solution
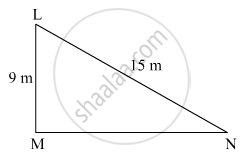
Let LN be the ladder of length 15 m that is resting against a wall. Let M be the base of the wall and L be the position of the window.
The window is 9 m above the ground. Now, MN is the distance between the base of the wall and that of the ladder.
In the right-angled triangle LMN, ∠M = 90°. Hence, side LN is the hypotenuse.
According to Pythagoras' theorem,
l(LN)2 = l(MN)2 + l(LM)2
⇒ (15)2 = l(MN)2 + (9)2
⇒ 225 = l(MN)2 + 81
⇒ l(MN)2 = 225 − 81
⇒ l(MN)2 = 144
⇒ l(MN)2 = (12)2
⇒ l(MN) = 12
∴ Length of seg MN = 12 m.
Hence, the distance between the base of the wall and that of the ladder is 12 m.
RELATED QUESTIONS
A man goes 10 m due east and then 24 m due north. Find the distance from the starting point
Sides of triangles are given below. Determine it is a right triangles? In case of a right triangle, write the length of its hypotenuse. 3 cm, 8 cm, 6 cm
Find the side and perimeter of a square whose diagonal is 10 cm.
In ∆ABC, seg AD ⊥ seg BC, DB = 3CD.
Prove that: 2AB2 = 2AC2 + BC2

In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

In ∆ ABC, AD ⊥ BC.
Prove that AC2 = AB2 +BC2 − 2BC x BD
Triangle ABC is right-angled at vertex A. Calculate the length of BC, if AB = 18 cm and AC = 24 cm.
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OE2 - OF2
To get from point A to point B you must avoid walking through a pond. You must walk 34 m south and 41 m east. To the nearest meter, how many meters would be saved if it were possible to make a way through the pond?
In a right angled triangle, the hypotenuse is the greatest side
