Advertisements
Advertisements
Question
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OE2 - OF2
Solution
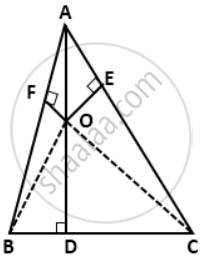
In right triangle OFA, ODB and OEC, we have
OA2 = AF2 + OF2
OB2 = BD2 + OD2
OC2 = CE2 + OE2
Adding all these results, we get
OA2 + OB2 + OC2 = AF2 + BD2 + CE2 + OF2 + OD2 + OE2
⇒ AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OE2 - OF2.
APPEARS IN
RELATED QUESTIONS
Side of a triangle is given, determine it is a right triangle.
`(2a – 1) cm, 2\sqrt { 2a } cm, and (2a + 1) cm`
A man goes 10 m due east and then 24 m due north. Find the distance from the starting point
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AD2 = BD × CD

Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Identify, with reason, if the following is a Pythagorean triplet.
(11, 60, 61)
In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2) = (AB2 + PQ2)
If the angles of a triangle are 30°, 60°, and 90°, then shown that the side opposite to 30° is half of the hypotenuse, and the side opposite to 60° is `sqrt(3)/2` times of the hypotenuse.
Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
Triangle ABC is right-angled at vertex A. Calculate the length of BC, if AB = 18 cm and AC = 24 cm.
Find the Pythagorean triplet from among the following set of numbers.
4, 5, 6
The foot of a ladder is 6m away from a wall and its top reaches a window 8m above the ground. If the ladder is shifted in such a way that its foot is 8m away from the wall to what height does its tip reach?
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9BP2 = 9BC2 + 4AC2
Find the unknown side in the following triangles
An isosceles triangle has equal sides each 13 cm and a base 24 cm in length. Find its height
The hypotenuse of a right angled triangle of sides 12 cm and 16 cm is __________
In the adjoining figure, a tangent is drawn to a circle of radius 4 cm and centre C, at the point S. Find the length of the tangent ST, if CT = 10 cm.

In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
