Advertisements
Advertisements
Question
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Solution
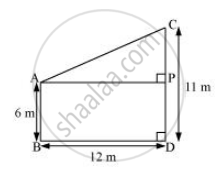
Let CD and AB be the poles of height 11 m and 6 m.
Therefore, CP = 11 − 6 = 5 m
From the figure, it can be observed that AP = 12m
Applying Pythagoras theorem for ΔAPC, we obtain
AP2 + PC2 = AC2
(12 m)2 + (5m)2 = (AC)2
AC2 = (144 + 25)m2 = 169 m2
AC = 13m
Therefore, the distance between their tops is 13 m.
APPEARS IN
RELATED QUESTIONS
ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ABC is a right triangle.
Which of the following can be the sides of a right triangle?
2 cm, 2 cm, 5 cm
In the case of right-angled triangles, identify the right angles.
Find the length of the hypotenuse of a right angled triangle if remaining sides are 9 cm and 12 cm.

In ΔMNP, ∠MNP = 90˚, seg NQ ⊥ seg MP, MQ = 9, QP = 4, find NQ.
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m;
find the distance between their tips.
In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC.

Diagonals of rhombus ABCD intersect each other at point O.
Prove that: OA2 + OC2 = 2AD2 - `"BD"^2/2`
In the given figure. PQ = PS, P =R = 90°. RS = 20 cm and QR = 21 cm. Find the length of PQ correct to two decimal places.
From given figure, In ∆ABC, If AC = 12 cm. then AB =?

Activity: From given figure, In ∆ABC, ∠ABC = 90°, ∠ACB = 30°
∴ ∠BAC = `square`
∴ ∆ABC is 30° – 60° – 90° triangle
∴ In ∆ABC by property of 30° – 60° – 90° triangle.
∴ AB = `1/2` AC and `square` = `sqrt(3)/2` AC
∴ `square` = `1/2 xx 12` and BC = `sqrt(3)/2 xx 12`
∴ `square` = 6 and BC = `6sqrt(3)`
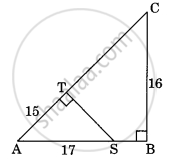
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.