Advertisements
Advertisements
Question
Diagonals of rhombus ABCD intersect each other at point O.
Prove that: OA2 + OC2 = 2AD2 - `"BD"^2/2`
Solution
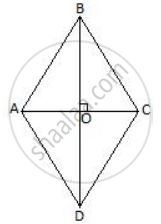
Diagonals of the rhombus are perpendicular to each other.
In quadrilateral ABCD, ∠AOD = ∠COD = 90°.
So, ΔAOD and ΔCOD are right-angled triangles.
In ΔAOD using Pythagoras theorem,
AD2 = OA2 + OD2
⇒ OA2 = AD2 - OD2 ....(i)
In ΔCOD using Pythagoras theorem,
CD2 = OC2 + OD2
⇒ OC2 = CD2 - OD2 ....(ii)
LHS = OA2 + OC2
= AD2 - OD2 + CD2 - OD2 ...[ From(i) and (ii) ]
= AD2 + CD2 - 2OD2
= AD2 + AD2 - 2`("BD"/2)^2` ...[ AD = CD and OD = `"BD"/2`]
= 2AD2 - `("BD")^2/2`
= RHS.
APPEARS IN
RELATED QUESTIONS
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Identify, with reason, if the following is a Pythagorean triplet.
(3, 5, 4)
Find the length diagonal of a rectangle whose length is 35 cm and breadth is 12 cm.
In ∆ABC, AB = 10, AC = 7, BC = 9, then find the length of the median drawn from point C to side AB.
Digonals of parallelogram WXYZ intersect at point O. If OY =5, find WY.
A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.
AD is drawn perpendicular to base BC of an equilateral triangle ABC. Given BC = 10 cm, find the length of AD, correct to 1 place of decimal.
In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
Triangle XYZ is right-angled at vertex Z. Calculate the length of YZ, if XY = 13 cm and XZ = 12 cm.
A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
Find the Pythagorean triplet from among the following set of numbers.
4, 5, 6
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.
Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
Find the distance between the helicopter and the ship
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
Lengths of sides of a triangle are 3 cm, 4 cm and 5 cm. The triangle is ______.
