Advertisements
Advertisements
Question
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
Solution
Let BC = 18 m be the flag pole and its shadow be AB = 9.6 m.
The distance of the top of the pole, C from the far end i.e., A of the shadow is AC.
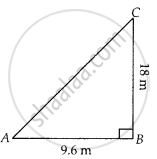
In right angled ∆ABC,
AC2 = AB2 + BC2 ...[By pythagoras theorem]
⇒ AC2 = (9.6)2 + (18)2
⇒ AC2 = 92.16 + 324
⇒ AC2 = 416.16
∴ AC = `sqrt(416.16)` = 20.4 m
Hence, the required distance is 20.4 m.
APPEARS IN
RELATED QUESTIONS
In ∆ABC, AB = 10, AC = 7, BC = 9, then find the length of the median drawn from point C to side AB.
In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC.

In Fig. 3, ∠ACB = 90° and CD ⊥ AB, prove that CD2 = BD x AD.

If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2 ) = (AB2 + PQ2)
The sides of a certain triangle is given below. Find, which of them is right-triangle
16 cm, 20 cm, and 12 cm
Find the length of the perpendicular of a triangle whose base is 5cm and the hypotenuse is 13cm. Also, find its area.
From given figure, In ∆ABC, If AC = 12 cm. then AB =?

Activity: From given figure, In ∆ABC, ∠ABC = 90°, ∠ACB = 30°
∴ ∠BAC = `square`
∴ ∆ABC is 30° – 60° – 90° triangle
∴ In ∆ABC by property of 30° – 60° – 90° triangle.
∴ AB = `1/2` AC and `square` = `sqrt(3)/2` AC
∴ `square` = `1/2 xx 12` and BC = `sqrt(3)/2 xx 12`
∴ `square` = 6 and BC = `6sqrt(3)`
Sides AB and BE of a right triangle, right-angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is ______.

In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
