Advertisements
Advertisements
Question
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2 ) = (AB2 + PQ2)
Solution
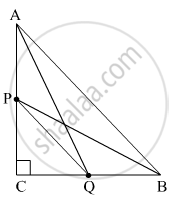
Using the Pythagoras theorem in ΔABC, ΔACQ, ΔBPC, ΔPCQ, we get
AB2 = AC2 + BC2 ......(1)
AQ2 = AC2 + CQ2 ......(2)
BP2 = PC2 + BC2 .......(3)
PQ2 = PC2 + CQ2 .......(4)
Adding the equations (2) and (3) we get
AQ2 + BP2 = AC2 + CQ2 + PC2 + BC2
= (AC2 + BC2) + (CQ + PC2)
= AB2 + PQ2
As
L.H.S. = AQ2 + BP2
= AB2 + PQ2
= R.H.S
Hence Proved
RELATED QUESTIONS
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
The perpendicular AD on the base BC of a ∆ABC intersects BC at D so that DB = 3 CD. Prove that `2"AB"^2 = 2"AC"^2 + "BC"^2`
Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
Find the Pythagorean triplet from among the following set of numbers.
3, 4, 5
The sides of the triangle are given below. Find out which one is the right-angled triangle?
40, 20, 30
Find the unknown side in the following triangles
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
In a right-angled triangle ABC, if angle B = 90°, then which of the following is true?
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
