Advertisements
Advertisements
Question
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
Advertisements
Solution
As the park is rectangular, all the angles area of 90°
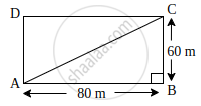
In right angled ΔABC,
AC2 = AB2 + BC2 ...[By Pythagoras theorem]
⇒ AC2 = (60)2 + (80)2 = 3600 + 6400
⇒ AC2 = 10000
⇒ AC = `sqrt(10000)`
⇒ AC = 100 m
If she goes through AB and AC, then the total distance covered = (60 + 80) m = 140 m
∴ Difference between two paths = (140 – 100) m = 40 m.
APPEARS IN
RELATED QUESTIONS
The points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right traingle ,right-angled at B. Find the values of p.
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after `1 1/2` hours?
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
Which of the following can be the sides of a right triangle?
2.5 cm, 6.5 cm, 6 cm
In the case of right-angled triangles, identify the right angles.
In ΔABC, Find the sides of the triangle, if:
- AB = ( x - 3 ) cm, BC = ( x + 4 ) cm and AC = ( x + 6 ) cm
- AB = x cm, BC = ( 4x + 4 ) cm and AC = ( 4x + 5) cm
The sides of a certain triangle is given below. Find, which of them is right-triangle
16 cm, 20 cm, and 12 cm
In the given figure, angle ADB = 90°, AC = AB = 26 cm and BD = DC. If the length of AD = 24 cm; find the length of BC.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2AD2 + `(1)/(2)"BC"^2`
Jiya walks 6 km due east and then 8 km due north. How far is she from her starting place?
