Advertisements
Advertisements
Question
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
Solution
Correct answer: A
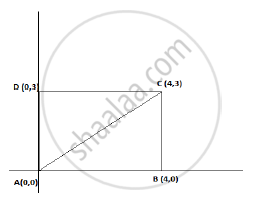
We see that AB = 4 units and BC = 3 units
Using Pythagoras theorem
AC2= AB2+ BC2
=42 + 32
AC 2 =25
Thus AC = 5 units
Hence length of the diagonal of the rectangle is 5 units
APPEARS IN
RELATED QUESTIONS
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder
In the given figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2 = AB2 + BC2 − 2BC.BD.

Prove that, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the square of remaining two sides
In triangle ABC, AB = AC = x, BC = 10 cm and the area of the triangle is 60 cm2.
Find x.
Choose the correct alternative:
In right-angled triangle PQR, if hypotenuse PR = 12 and PQ = 6, then what is the measure of ∠P?
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then ______.
In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
Two squares are congruent, if they have same ______.
