Advertisements
Advertisements
Question
A chord of a circle of radius 10 em subtends a right angle at its centre. The length of the chord (in em) is
`(A) 5sqrt 2`
`(B) 10 sqrt2`
`(C)5/sqrt2`
`(D) 10sqrt 3`
Solution
Correct answer: B
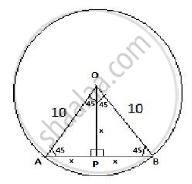
Given ∠ AOB is given as 90º
ΔAOB is an isosceles triangle since OA = OB
Therefore ∠OAB = ∠OBA = 45º
Thus ∠ AOP = 45º and ∠ BOP = 45º
Hence ΔAOP and ΔBOP also are isosceles triangles
AP = OP and OP PB
In ΔAOP
x2 + x2 = 102 [Pythagoras theorem]
Thus 2 x2 = 100
x=5√2
Hence length of chord AB = 2 x = 5√2+5√2=10√2
APPEARS IN
RELATED QUESTIONS
In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.
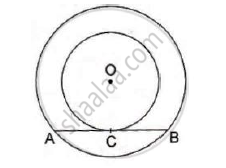
In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
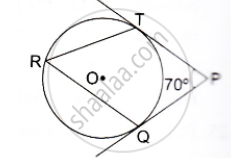
In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70° , find the ∠TRQ.
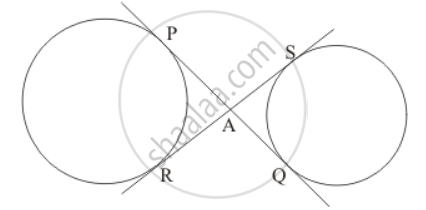
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
Find the area of a circle of radius 7 cm.
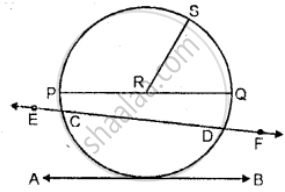
Use the figure given below to fill in the blank:
________ is a radius of the circle.
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).

If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is ______.
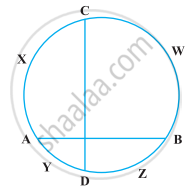
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.