Advertisements
Advertisements
Question
In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70° , find the ∠TRQ.
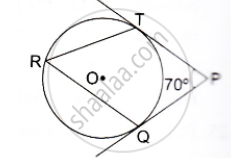
Solution
Construction: Join OQ and OT
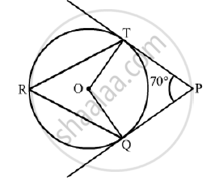
We know that the radius and tangent are perpendicular at their point of contact
∵ ∠OTP = ∠OQP = 90°
Now, In quadrilateral OQPT
∠QOT + ∠OTP +∠OQP+ ∠TPO = 360° [Angle sum property of a quadrilateral]
⇒ ∠QOT +90° + 90°+ 70° = 360°
⇒ 250° + ∠QOT = 360°
⇒ ∠ QOT = 110°
We know that the angle subtended by an arc at the center is double the angle subtended by the arc at any point on the remaining part of the circle.
`∴ ∠ TRQ = 1/2 (∠QOT ) = 55°`
RELATED QUESTIONS
Find the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
Write True or False. Give reason for your answer.
A circle is a plane figure.
In two concentric circles, a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm, then find the radius of the smaller circle.
In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 1760 cm |
Find the diameter of the circle
Radius = 8 cm
Find the diameter of the circle
Radius = 6 cm
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.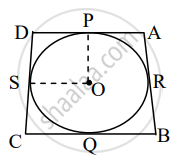
C(O, r1) and C(O, r2) are two concentric circles with r1 > r2 AB is a chord of C(O, r1) touching C(O, r2) at C then ______
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
