Advertisements
Advertisements
Question
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 1760 cm |
Solution
Given: Circumference C = 1760 cm
2πr = 1760
`2 xx 22/7 xx "r"` = 1760
r = `(1760 xx 7)/(2 xx 22)`
= `(160 xx 7)/(2 xx 2)`
= 40 × 7
= 280 cm
diameter = 2 × r
= 2 × 280
= 560 cm
Tabulating the results
| radius (r) | diameter (d) | Circumference (C) |
| 280 cm | 560 cm | 1760 cm |
APPEARS IN
RELATED QUESTIONS
Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). Find the values of y. Hence find the radius of the circle.
In the given figure, PQ is a chord of length 8cm of a circle of radius 5cm. The tangents at P and Q intersect at a point T. Find the length TP

A point P is 26 cm away from O of circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
true or false
A chord of a circle, which is twice as long is its radius is a diameter of the circle.
In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.

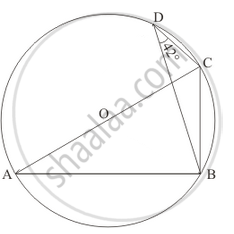
In the given figure, O is the centre of the circle and ∠BDC = 42°. The measure of ∠ACB is
Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
Draw a circle of radius 4.8 cm and mark its center as P.
(i) Draw radii PA and PB such that ∠APB = 45°.
(ii) Shade the major sector of the circle
Draw circle with the radii given below.
4 cm
In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4 cm. The radius of the circle is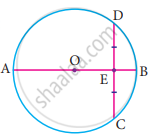
Find the diameter of the circle
Radius = 6 cm
If the angle between two radii of a circle is 130°, then the angle between the tangents at the ends of the radii is ______
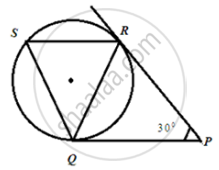
In the following figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, then ∠RQS.
If a number of circles pass through the endpoints P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
The circumcentre of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90º.
From the figure, identify three radii.