Advertisements
Advertisements
Question
In the given figure, O is the centre of the circle and ∠BDC = 42°. The measure of ∠ACB is
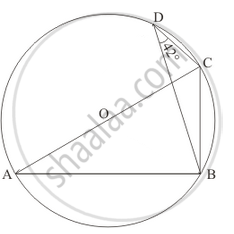
Options
42°
48°
58°
52°
Solution
48°
Construction: Join A and D.
Since AC is the diameter. So ∠ADC will be 90°.
Therefore,
`angleADB = 90 - angleBDC`
= 90 - 42
`angle ADB = 48°`
∠ACB = ∠ADB = 48° (Angle in the same segment are equal.)
APPEARS IN
RELATED QUESTIONS
Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle, is bisected at the point of contact.
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
O is the center of a circle of radius 8cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
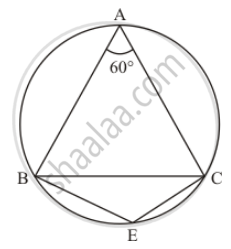
In the given figure, ΔABC is an equilateral triangle. Find m∠BEC.
Find the length of the chord of a circle in the following when:
Radius is 6.5 cm and the distance from the centre is 2.5 cm
Use the figure given below to fill in the blank:
If the length of RS is 5 cm, the length of PQ = _______

In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).

If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
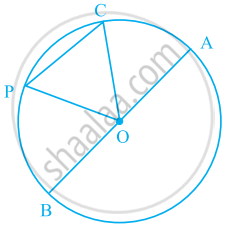
In the given figure, O is the centre of the circle. Name all radii of the circle.