Advertisements
Advertisements
Question
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
Solution
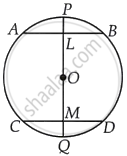
Given: AB and CD are two chords of a circle whose centre is O and PQ is a diameter bisecting the chord AB and CD at L and M, respectively and the diameter PQ passes through the centre O of the circle.
To prove: AB || CD
Proof: Since, L is the mid-point of AB.
∴ OL ⊥ AB ...[Since, the line joining the centre of a circle to the mid-point of a chord is perpendicular to the chord]
⇒ ∠ALO = 90° ...(i)
Similarly, OM ⊥ CD
∴ ∠OMD = 90° ...(ii)
From equations (i) and (ii),
∠ALO = ∠OMD = 90°
But, these are alternating angles.
So, AB || CD
Hence proved.
APPEARS IN
RELATED QUESTIONS
Fill in the blanks:
The centre of a circle lies in ____________ of the circle.
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
In the fig. a circle is inscribed in a quadrilateral ABCD in which ∠B = 90° if AD = 23cm,
AB = 29cm and DS = 5cm, find the radius of the circle.
Prove that two different circles cannot intersect each other at more than two points.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
In the given figure, a ∆ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the lengths of sides AB and AC, when area of ∆ABC is 84 cm2.

Use the figure given below to fill in the blank:
________ is a radius of the circle.
Construct a triangle ABC with AB = 5 cm, ∠B = 60° and BC = 6. 4 cm. Draw the incircle of the triangle ABC.
The center of a circle is at point O and its radius is 8 cm. State the position of a point P (point P may lie inside the circle, on the circumference of the circle, or outside the circle), when:
(a) OP = 10.6 cm
(b) OP = 6.8 cm
(c) OP = 8 cm
State, if the following statement is true or false:
The diameters of a circle always pass through the same point in the circle.
