Advertisements
Chapters
2: Polynomials
3: Coordinate Geometry
4: Linear Equation In Two Variables
5: Introduction To Euclid's Geometry
6: Lines & Angles
7: Triangles
8: Quadrilaterals
9: Areas of Parallelograms & Triangles
▶ 10: Circles
11: Construction
12: Heron's Formula
13: Surface Area & Volumes
14: Statistics & Probability
![NCERT Exemplar solutions for Mathematics [English] Class 9 chapter 10 - Circles NCERT Exemplar solutions for Mathematics [English] Class 9 chapter 10 - Circles - Shaalaa.com](/images/mathematics-english-class-9_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 10: Circles
Below listed, you can find solutions for Chapter 10 of CBSE NCERT Exemplar for Mathematics [English] Class 9.
NCERT Exemplar solutions for Mathematics [English] Class 9 10 Circles Exercise 10.1 [Pages 99 - 101]
Choose the correct alternative:
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
17 cm
15 cm
4 cm
8 cm
In the following figure, if OA = 5 cm, AB = 8 cm and OD is perpendicular to AB, then CD is equal to ______.
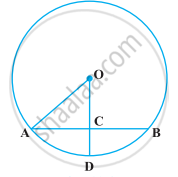
2 cm
3 cm
4 cm
5 cm
If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is ______.
6 cm
8 cm
10 cm
12 cm
In the following figure, if ∠ABC = 20º, then ∠AOC is equal to ______.
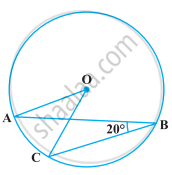
20º
40º
60º
10º
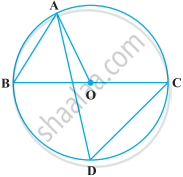
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

30º
60º
90º
45º
In the following figure, if ∠OAB = 40º, then ∠ACB is equal to ______.
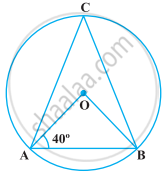
50º
40º
60º
70°
In the following figure, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to ______.
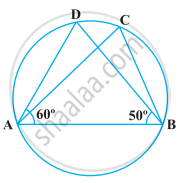
60º
50º
70º
80º
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to ______.
80º
50º
40º
30º
In the following figure, BC is a diameter of the circle and ∠BAO = 60º. Then ∠ADC is equal to ______.
30º
45º
60º
120º
In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to ______.

30º
45º
90º
60º
NCERT Exemplar solutions for Mathematics [English] Class 9 10 Circles Exercise 10.2 [Pages 101 - 102]
State whether the following statement is True or False:
Two chords AB and CD of a circle are each at distances 4 cm from the centre. Then AB = CD.
True
False
Two chords AB and AC of a circle with centre O are on the opposite sides of OA. Then ∠OAB = ∠OAC .
True
False
Two congruent circles with centres O and O′ intersect at two points A and B. Then ∠AOB = ∠AO′B.
True
False
Through three collinear points a circle can be drawn.
True
False
A circle of radius 3 cm can be drawn through two points A, B such that AB = 6 cm.
True
False
If AOB is a diameter of a circle and C is a point on the circle, then AC2 + BC2 = AB2.
True
False
ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
True
False
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
True
False
If A, B, C and D are four points such that ∠BAC = 45° and ∠BDC = 45°, then A, B, C, D are concyclic.
True
False
In the following figure, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.
True
False
NCERT Exemplar solutions for Mathematics [English] Class 9 10 Circles Exercise 10.3 [Pages 103 - 105]
If arcs AXB and CYD of a circle are congruent, find the ratio of AB and CD.
If the perpendicular bisector of a chord AB of a circle PXAQBY intersects the circle at P and Q, prove that arc PXA ≅ arc PYB.
A, B and C are three points on a circle. Prove that the perpendicular bisectors of AB, BC and CA are concurrent.
AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
ABCD is such a quadrilateral that A is the centre of the circle passing through B, C and D. Prove that ∠CBD + ∠CDB = `1/2` ∠BAD
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.
If BM and CN are the perpendiculars drawn on the sides AC and AB of the triangle ABC, prove that the points B, C, M and N are concyclic.
If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral so formed is cyclic.
If a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are also equal.
The circumcentre of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90º.
A chord of a circle is equal to its radius. Find the angle subtended by this chord at a point in major segment.
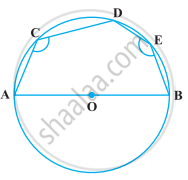
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

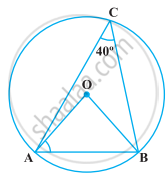
In the following figure, ∠ACB = 40º. Find ∠OAB.
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
Two circles with centres O and O′ intersect at two points A and B. A line PQ is drawn parallel to OO′ through A(or B) intersecting the circles at P and Q. Prove that PQ = 2 OO′.
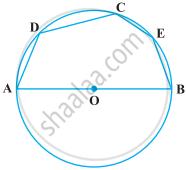
In the following figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.
In the following figure, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

NCERT Exemplar solutions for Mathematics [English] Class 9 10 Circles Exercise 10.4 [Pages 106 - 107]
If two equal chords of a circle intersect, prove that the parts of one chord are separately equal to the parts of the other chord.
If non-parallel sides of a trapezium are equal, prove that it is cyclic.
If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.
ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.
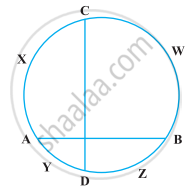
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
In the following figure, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = `1/2` (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).
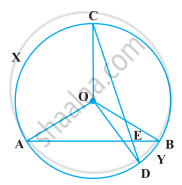
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
A circle has radius `sqrt(2)` cm. It is divided into two segments by a chord of length 2 cm. Prove that the angle subtended by the chord at a point in major segment is 45°.
Two equal chords AB and CD of a circle when produced intersect at a point P. Prove that PB = PD.
AB and AC are two chords of a circle of radius r such that AB = 2AC. If p and q are the distances of AB and AC from the centre, prove that 4q2 = p2 + 3r2.
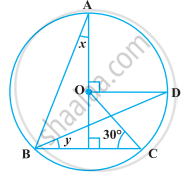
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.
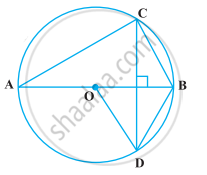
In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.
Solutions for 10: Circles
![NCERT Exemplar solutions for Mathematics [English] Class 9 chapter 10 - Circles NCERT Exemplar solutions for Mathematics [English] Class 9 chapter 10 - Circles - Shaalaa.com](/images/mathematics-english-class-9_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
NCERT Exemplar solutions for Mathematics [English] Class 9 chapter 10 - Circles
Shaalaa.com has the CBSE Mathematics Mathematics [English] Class 9 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. NCERT Exemplar solutions for Mathematics Mathematics [English] Class 9 CBSE 10 (Circles) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. NCERT Exemplar textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 9 chapter 10 Circles are Angle Subtended by a Chord at a Point, Perpendicular from the Centre to a Chord, Equal Chords and Their Distances from the Centre, Angle Subtended by an Arc of a Circle, Concept of Circle, Cyclic Quadrilateral, Circles Passing Through One, Two, Three Points.
Using NCERT Exemplar Mathematics [English] Class 9 solutions Circles exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in NCERT Exemplar Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [English] Class 9 students prefer NCERT Exemplar Textbook Solutions to score more in exams.
Get the free view of Chapter 10, Circles Mathematics [English] Class 9 additional questions for Mathematics Mathematics [English] Class 9 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.
