Advertisements
Advertisements
Question
In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to ______.

Options
30º
45º
90º
60º
Solution
In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to 60º.
Explanation:

Since, the angle subtended by an arc at the centre is twice the angle subtended by it at any point on the remaining part of the circle.
∴ ∠AOB = 2∠ACB
`\implies` 90° = 2∠ACB ...[∵ ∠AOB = 90°]
`\implies` ∠ACB = 45°
Also, AO = OB ...[Radii of the same circle]
`\implies` ∠ABO = ∠BAO ...(i) [Angles opposite to equal sides are equal]
Now, in ΔOAB, ∠OAB + ∠ABO + ∠BOA = 180° ...[Sum of angles of a triangle is 180°]
∴ ∠OAB + ∠OAB + 90° = 180° ...[From (i)]
`\implies` 2∠OAB = 180° – 90° = 90°
`\implies ∠OAB = 90^circ/2 = 45^circ` ...(ii)
Also, in ΔACB, ∠ACB + ∠CBA + ∠CAB = 180° ...[Sum of angles of a triangle is 180°]
∴ 45° + 30° + ∠CAB = 180° ...[∵ ∠ABC = 30°]
`\implies` ∠CAB = 105°
Since, ∠CAO + ∠OAB = ∠CAB
`\implies` ∠CAO + 45° = 105° ...[From (ii)]
`\implies` ∠CAO = 105° – 45° = 60°
APPEARS IN
RELATED QUESTIONS
In Fig., if AB = AC, prove that BE = EC
Fill in the blanks:
The centre of a circle lies in ____________ of the circle.
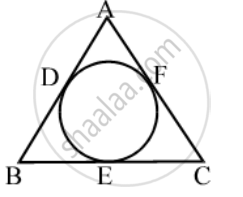
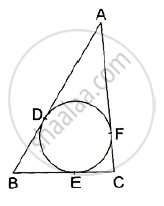
In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14cm, BC = 8cm and CA=12 cm. Find the length AD, BE and CF.
Find the area of a circle of radius 7 cm.
Construct a triangle XYZ in which XY = YZ= 4.5 cm and ZX = 5.4 cm. Draw the circumcircle of the triangle and measure its circumradius.
Can the length of a chord of a circle be greater than its diameter ? Explain.
In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).

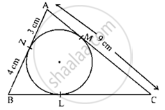
In the adjoining figure, Δ ABC is circumscribing a circle. Then, the length of BC is ______
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure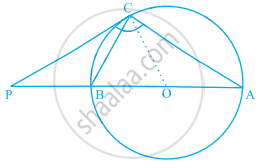
From the figure, identify a segment.

