Advertisements
Advertisements
प्रश्न
In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to ______.

पर्याय
30º
45º
90º
60º
उत्तर
In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to 60º.
Explanation:

Since, the angle subtended by an arc at the centre is twice the angle subtended by it at any point on the remaining part of the circle.
∴ ∠AOB = 2∠ACB
`\implies` 90° = 2∠ACB ...[∵ ∠AOB = 90°]
`\implies` ∠ACB = 45°
Also, AO = OB ...[Radii of the same circle]
`\implies` ∠ABO = ∠BAO ...(i) [Angles opposite to equal sides are equal]
Now, in ΔOAB, ∠OAB + ∠ABO + ∠BOA = 180° ...[Sum of angles of a triangle is 180°]
∴ ∠OAB + ∠OAB + 90° = 180° ...[From (i)]
`\implies` 2∠OAB = 180° – 90° = 90°
`\implies ∠OAB = 90^circ/2 = 45^circ` ...(ii)
Also, in ΔACB, ∠ACB + ∠CBA + ∠CAB = 180° ...[Sum of angles of a triangle is 180°]
∴ 45° + 30° + ∠CAB = 180° ...[∵ ∠ABC = 30°]
`\implies` ∠CAB = 105°
Since, ∠CAO + ∠OAB = ∠CAB
`\implies` ∠CAO + 45° = 105° ...[From (ii)]
`\implies` ∠CAO = 105° – 45° = 60°
APPEARS IN
संबंधित प्रश्न
ABCD is a quadrilateral such that ∠D = 90°. A circle (O, r) touches the sides AB, BC, CD and DA at P,Q,R and If BC = 38 cm, CD = 25 cm and BP = 27 cm, find r.
In the given figure, O is the centre of the circle. PA and PB are tangents. Show that AOBP is cyclic quadrilateral.

In the given figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.

An equilateral triangle ABC is inscribed in a circle with centre O. The measures of ∠BOCis
AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 1760 cm |
Find the radius of the circle
Diameter = 76 cm
If O is the center of the circle in the figure alongside, then complete the table from the given information.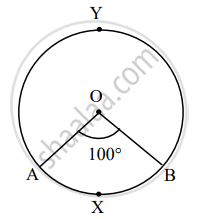
The type of arc
| Type of circular arc | Name of circular arc | Measure of circular arc |
| Minor arc | ||
| Major arc |
Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
