Advertisements
Advertisements
प्रश्न
In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to ______.

विकल्प
30º
45º
90º
60º
उत्तर
In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to 60º.
Explanation:

Since, the angle subtended by an arc at the centre is twice the angle subtended by it at any point on the remaining part of the circle.
∴ ∠AOB = 2∠ACB
`\implies` 90° = 2∠ACB ...[∵ ∠AOB = 90°]
`\implies` ∠ACB = 45°
Also, AO = OB ...[Radii of the same circle]
`\implies` ∠ABO = ∠BAO ...(i) [Angles opposite to equal sides are equal]
Now, in ΔOAB, ∠OAB + ∠ABO + ∠BOA = 180° ...[Sum of angles of a triangle is 180°]
∴ ∠OAB + ∠OAB + 90° = 180° ...[From (i)]
`\implies` 2∠OAB = 180° – 90° = 90°
`\implies ∠OAB = 90^circ/2 = 45^circ` ...(ii)
Also, in ΔACB, ∠ACB + ∠CBA + ∠CAB = 180° ...[Sum of angles of a triangle is 180°]
∴ 45° + 30° + ∠CAB = 180° ...[∵ ∠ABC = 30°]
`\implies` ∠CAB = 105°
Since, ∠CAO + ∠OAB = ∠CAB
`\implies` ∠CAO + 45° = 105° ...[From (ii)]
`\implies` ∠CAO = 105° – 45° = 60°
APPEARS IN
संबंधित प्रश्न
In the given figure, PQ and RS are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersects PQ at A and RS at B. Prove that ∠AOB = 90º
If the quadrilateral sides touch the circle prove that sum of pair of opposite sides is equal to the sum of other pair.
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

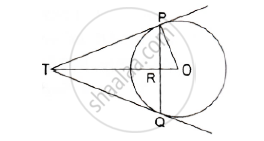
PQ is a chord of length 4.8 cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
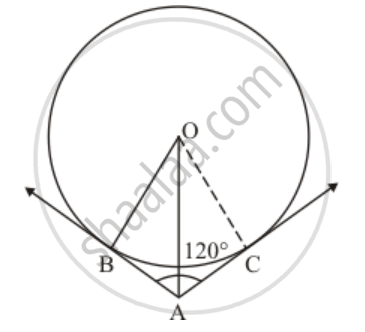
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
Construct a triangle PQR with QR = 5.5 cm, ∠Q = 60° and angle R = 45°. Construct the circumcircle cif the triangle PQR.
Find the radius of the circle
Diameter = 30 cm
Say true or false:
The centre of a circle is always in its interior.
