Advertisements
Advertisements
प्रश्न
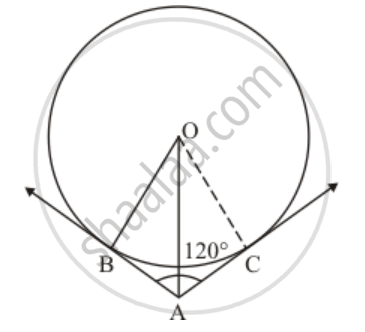
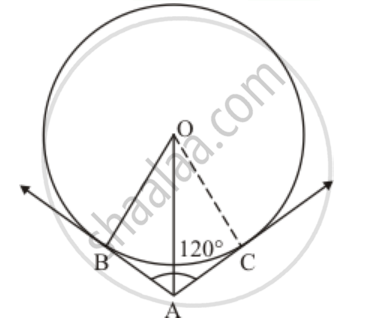
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
उत्तर
Consider Δ OAB and Δ OAC.
We have,
OB = OC (Since they are radii of the same circle)
AB = AC (Since length of two tangents drawn from an external point will be equal)
OA is the common side.
Therefore by SSS congruency, we can say that Δ OAB and Δ OAC are congruent triangles.
Therefore,
∠OAC = ∠OAC
It is given that,
`∠OAB +∠OAC=120^o`
`2∠OAB=120^o`
`∠OAB=60^o`
We know that,
`cos∠OAB =(AB)/(OA) `
`cos 60^o =(AB)/(OA) `
We know that,
`cos 60^o =1/2`
Therefore,
`1/2=(AB)/(OA)`
OA = 2AB
APPEARS IN
संबंधित प्रश्न
In fig. XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that, XA + AR = XB + BR.
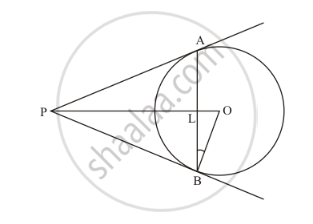
In the given figure, AB is a chord of length 16 cm of a circle of radius 10 cm. The tangents at A and B intersect at a point P. Find the length of PA.
ture or false v
The degree measure of a semi-circle is 180°.
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
- ∠AOB,
- ∠ACB,
- ∠ABC.
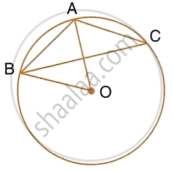
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
In a circle with centre P, chord AB is parallel to a tangent and intersects the radius drawn from the point of contact to its midpoint. If AB = `16sqrt(3)`, then find the radius of the circle
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
