Advertisements
Online Mock Tests
Chapters
2: Polynomials
3: Pair of Linear Equations in Two Variables
4: Quadratic Equations
5: Arithmetic Progression
6: Co-Ordinate Geometry
7: Triangles
▶ 8: Circles
9: Constructions
10: Trigonometric Ratios
11: Trigonometric Identities
12: Trigonometry
13: Areas Related to Circles
14: Surface Areas and Volumes
15: Statistics
16: Probability
![RD Sharma solutions for Mathematics [English] Class 10 chapter 8 - Circles RD Sharma solutions for Mathematics [English] Class 10 chapter 8 - Circles - Shaalaa.com](/images/8193647920-mathematics-english-class-10_6:5809898a5fef45e9a2f7e6b414d392fa.jpg)
Advertisements
Solutions for Chapter 8: Circles
Below listed, you can find solutions for Chapter 8 of CBSE RD Sharma for Mathematics [English] Class 10.
RD Sharma solutions for Mathematics [English] Class 10 8 Circles Exercise 8 [Page 37]
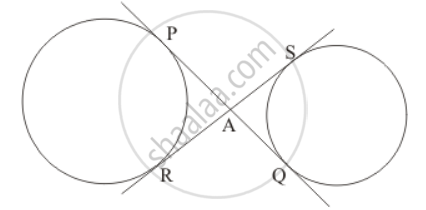
In Fig. 7, two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of `(DO')/(CO')`

In the fig. ABC is right triangle right angled at B such that BC = 6cm and AB = 8cm. Find the radius of its in circle.
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
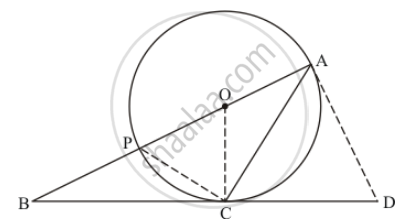
In fig.. O is the center of the circle and BCD is tangent to it at C. Prove that ∠BAC +
∠ACD = 90°
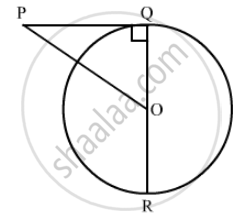
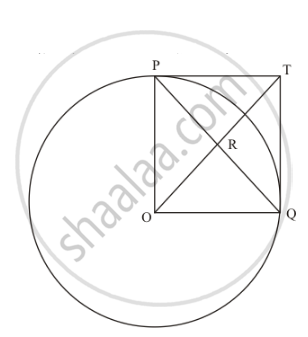
In the given figure, PO⊥QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OT are right bisector of each other.
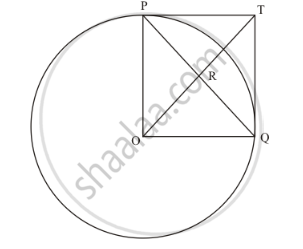
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO~Δ ABC.
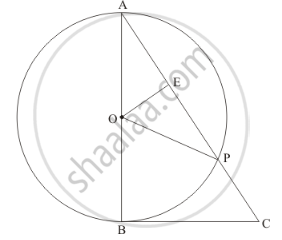
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
In fig common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
In figure OQ : PQ = 3 : 4 and perimeter of ΔPDQ = 60cm. determine PQ, QR and OP.
RD Sharma solutions for Mathematics [English] Class 10 8 Circles Exercise 8.1 [Page 5]
The common point of a tangent to a circle and the circle is called ______.
A circle can have ______ parallel tangents at the most.
A tangent to a circle intersects it in ______ point (s).
A line intersecting a circle in two points is called a ______.
Fill in the blank
The angle between tangent at a point on a circle and the radius through the point is ........
How many tangents can a circle have?
O is the center of a circle of radius 8cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB
If the tangent at point P to the circle with center O cuts a line through O at Q such that PQ= 24cm and OQ = 25 cm. Find the radius of circle
RD Sharma solutions for Mathematics [English] Class 10 8 Circles Exercise 8.2 [Pages 33 - 42]
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
Find the length of a tangent drawn to a circle with radius 5cm, from a point 13 cm from the center of the circle.
A point P is 26 cm away from O of circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
If from any point on the common chord of two intersecting circles, tangents be drawn to circles, prove that they are equal.
If the quadrilateral sides touch the circle prove that sum of pair of opposite sides is equal to the sum of other pair.
Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
If AB, AC, PQ are tangents in Fig. and AB = 5cm find the perimeter of ΔAPQ.
Prove that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at center.
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
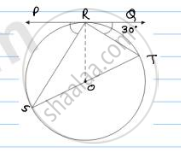
If PA and PB are tangents from an outside point P. such that PA = 10 cm and ∠APB = 60°. Find the length of chord AB.
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
From an external point P, tangents PA and PB are drawn to the circle with centre O. If CD is the tangent to the circle at point E and PA = 14 cm. Find the perimeter of ABCD.
In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
From a point P, two tangents PA and PB are drawn to a circle with center O. If OP =
diameter of the circle shows that ΔAPB is equilateral.
Two tangent segments PA and PB are drawn to a circle with center O such that ∠APB =120°. Prove that OP = 2AP
If Δ ABC is isosceles with AB = AC and C (O, r) is the incircle of the ΔABC touching BC at L,prove that L bisects BC.
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
In fig. a circle touches all the four sides of quadrilateral ABCD with AB = 6cm, BC = 7cm, CD = 4cm. Find AD.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Two circles touch externally at a point P. from a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and E respectively. Prove that TQ = TR.
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
In the fig. a circle is inscribed in a quadrilateral ABCD in which ∠B = 90° if AD = 23cm,
AB = 29cm and DS = 5cm, find the radius of the circle.
In fig. there are two concentric circles with Centre O of radii 5cm and 3cm. From an
external point P, tangents PA and PB are drawn to these circles if AP = 12cm, find the
tangent length of BP.
In the given figure, AB is a chord of length 16 cm of a circle of radius 10 cm. The tangents at A and B intersect at a point P. Find the length of PA.
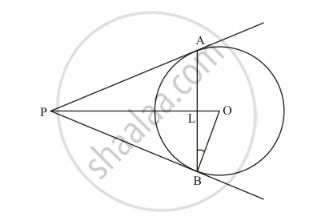
In figure PA and PB are tangents from an external point P to the circle with centre O. LN touches the circle at M. Prove that PL + LM = PN + MN
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF
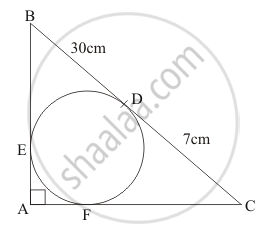
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (ii) radius of the circle.

If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
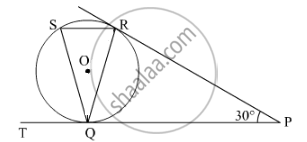
From an external point P , tangents PA = PB are drawn to a circle with centre O . If \[\angle PAB = {50}^o\] , then find \[\angle AOB\]
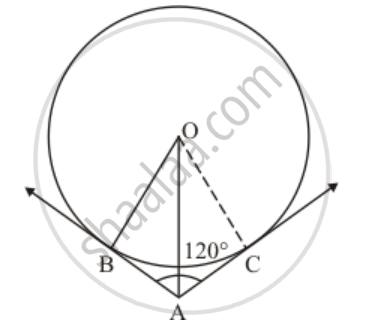
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
The length of three concesutive sides of a quadrilateral circumscribing a circle are 4 cm, 5 cm, and 7 cm respectively. Determine the length of the fourth side.
In figure, the common tangent, AB and CD to two circles with centres O and O' intersect at E. Prove that the points O, E, O' are collinear.
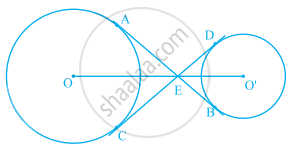
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
Two concentric circles are of diameters 30 cm and 18 cm. Find the length of the chord of the larger circle which touches the smaller circle.
AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure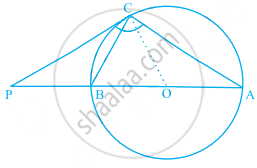
AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.
In the given figure, a ∆ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the lengths of sides AB and AC, when area of ∆ABC is 84 cm2.

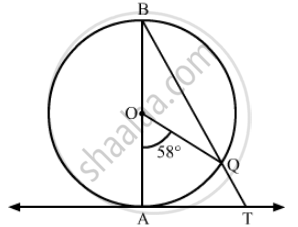
In the given figure, AB is a diameter of a circle with centre O and AT is a tangent. If \[\angle\] AOQ = 58º, find \[\angle\] ATQ.
In the given figure, OQ : PQ = 3.4 and perimeter of Δ POQ = 60 cm. Determine PQ, QR and OP.
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
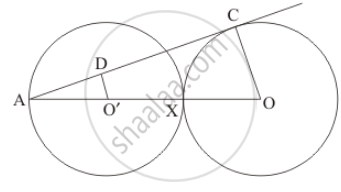
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO ∼ Δ ABC.
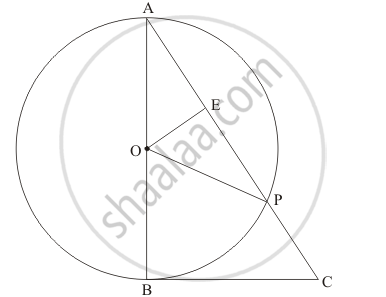
In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.
In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.
Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
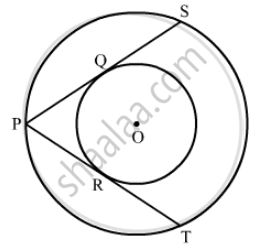
In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.

In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.
Solutions for 8: Circles
![RD Sharma solutions for Mathematics [English] Class 10 chapter 8 - Circles RD Sharma solutions for Mathematics [English] Class 10 chapter 8 - Circles - Shaalaa.com](/images/8193647920-mathematics-english-class-10_6:5809898a5fef45e9a2f7e6b414d392fa.jpg)
RD Sharma solutions for Mathematics [English] Class 10 chapter 8 - Circles
Shaalaa.com has the CBSE Mathematics Mathematics [English] Class 10 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. RD Sharma solutions for Mathematics Mathematics [English] Class 10 CBSE 8 (Circles) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. RD Sharma textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 10 chapter 8 Circles are Circles Passing Through One, Two, Three Points, Converse of Tangent Theorem, Tangent Segment Theorem, Inscribed Angle Theorem, Corollaries of Inscribed Angle Theorem, Theorem: Opposite angles of a cyclic quadrilateral are supplementary., Corollary of Cyclic Quadrilateral Theorem, Converse: If a Pair of Opposite Angles of a Quadrilateral is Supplementary, Then the Quadrilateral is Cyclic., Theorem of Angle Between Tangent and Secant, Converse of Theorem of the Angle Between Tangent and Secant, Theorem of Internal Division of Chords, Theorem of External Division of Chords, Tangent to a Circle, Number of Tangents from a Point on a Circle, Touching Circles, Concept of Circle, Secant and Tangent, Theorem of Touching Circles, Tangent Properties - If Two Circles Touch, the Point of Contact Lies on the Straight Line Joining Their Centers, Introduction to an Arc, Congruence of Arcs, Property of Sum of Measures of Arcs, Inscribed Angle, Intercepted Arc, Cyclic Quadrilateral, Converse of Cyclic Quadrilateral Theorem, Tangent Secant Segments Theorem, Tangent - Secant Theorem, Angle Subtended by the Arc to the Point on the Circle, Angle Subtended by the Arc to the Centre, Tangent to a Circle, Number of Tangents from a Point on a Circle, Concept of Circle.
Using RD Sharma Mathematics [English] Class 10 solutions Circles exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in RD Sharma Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [English] Class 10 students prefer RD Sharma Textbook Solutions to score more in exams.
Get the free view of Chapter 8, Circles Mathematics [English] Class 10 additional questions for Mathematics Mathematics [English] Class 10 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.
