Advertisements
Advertisements
प्रश्न
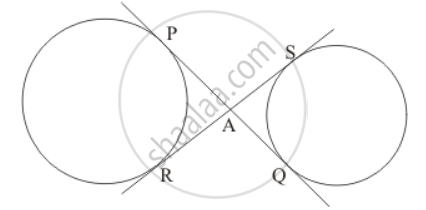
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
उत्तर
The figure given in the question is
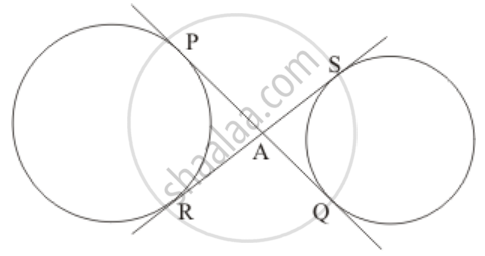
We know from the property of tangents that the length of two tangents drawn from a common external point will be equal. Therefore,
PA = RA …… (1)
AQ = AS …… (2)
Let us add equation (1) and (2)
PA + AQ = RA + AS
PQ = RS
Thus we have proved that PQ = RS.
APPEARS IN
संबंधित प्रश्न
In Fig. 1, the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is ?
In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

Use the figure given below to fill in the blank:
Tangent to a circle is _______.

Use the figure given below to fill in the blank:
AB is a ______ of the circle.

The diameter of a circle is 12.6 cm. State, the length of its radius.
If the angle between two radii of a circle is 130°, then the angle between the tangents at the ends of the radii is ______
If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.
