Advertisements
Advertisements
प्रश्न
In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

उत्तर
The given information can be diagrammatically represented as follows:
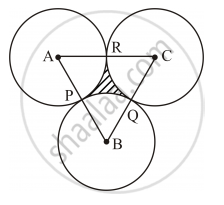
Here, A, B and C are the centres of the circles.
Radius of each circle, r = 3.5 cm
Thus, the measure of each of the sides of ΔABC is 3.5 cm + 3.5 cm = 7 cm.
Since the sides of triangle ABC are of equal lengths, it is an equilateral triangle.
∴ ∠A = ∠B = ∠C = 60°
Area of the shaded region = Area of ΔABC − (sum of areas of sectors APR, BPQ and CQR)
`=sqrt3/4a^2-3xxO//360^@xxpir`
`=1.732/4xx(7"cm")^2-3xx60^@/360^@xx22/7xx3.5"cm"xx3.5"cm"`
`=21.217 "cm"^2-19.25cm^2`
`=1.97"cm"^2`
APPEARS IN
संबंधित प्रश्न
From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
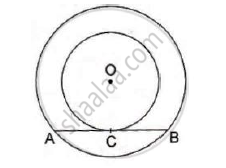
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.

In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
In the figure, O is the center of the circle. Line AQ is a tangent. If OP = 3, m(arc PM) = 120°, then find the length of AP.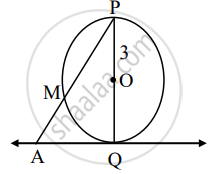
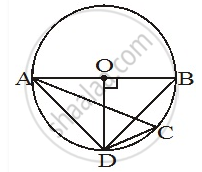
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD.