Advertisements
Advertisements
प्रश्न
In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

उत्तर
The given information can be diagrammatically represented as follows:
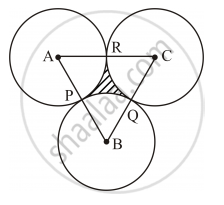
Here, A, B and C are the centres of the circles.
Radius of each circle, r = 3.5 cm
Thus, the measure of each of the sides of ΔABC is 3.5 cm + 3.5 cm = 7 cm.
Since the sides of triangle ABC are of equal lengths, it is an equilateral triangle.
∴ ∠A = ∠B = ∠C = 60°
Area of the shaded region = Area of ΔABC − (sum of areas of sectors APR, BPQ and CQR)
`=sqrt3/4a^2-3xxO//360^@xxpir`
`=1.732/4xx(7"cm")^2-3xx60^@/360^@xx22/7xx3.5"cm"xx3.5"cm"`
`=21.217 "cm"^2-19.25cm^2`
`=1.97"cm"^2`
APPEARS IN
संबंधित प्रश्न
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
Prove that two different circles cannot intersect each other at more than two points.
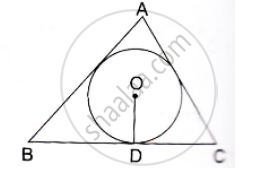
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4cm and 3cm respectively. If the area of 2 ABC 21cm then find the lengths of sides AB and AC.
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.

In following fig. ABC is an equilateral triangle . A circle is drawn with centre A so that ot cuts AB and AC at M and N respectively. Prove that BN = CM.

Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 24 m |
From the figure, identify a segment.

A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
Find the length of the arc of a circle which subtends an angle of 60° at the centre of the circle of radius 42 cm.
