Advertisements
Advertisements
प्रश्न
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4cm and 3cm respectively. If the area of 2 ABC 21cm then find the lengths of sides AB and AC.
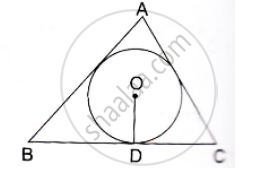
उत्तर
Construction: Join OA, OB, OC, OE ⊥ AB at E and OF ⊥ AC at F
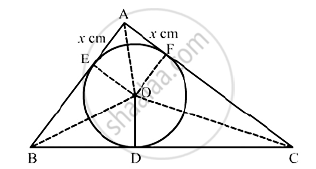
We know that tangent segments to a circle from the same external point are congruent
Now, we have
AE = AF,BD = BE = 4cmand CD = CF = 3cm
Now,
Area (ΔABC) = Area(ΔBOC)+ Area(ΔAOB) + Area(ΔAOC)
`⇒21 = 1/2 xx BC xx OD +1/2 xx AB xx OE +1/2 xx AC xx OF`
`⇒ 42 = 7 xx 2 + (4+x) xx 2 +(3+ x) xx2`
⇒ 21 = 7 + 4 + x + 3 + x
⇒ 21=14+2x
⇒ 2x =7
⇒ x= 3.5 cm
∴ AB = 4 + 3.5 = 7.5 cm and AC = 3 +3.5 = 6.5 cm
APPEARS IN
संबंधित प्रश्न
true or false
Sector is the region between the chord and its corresponding arc.
In the given figure, O is the centre of the circle. PA and PB are tangents. Show that AOBP is cyclic quadrilateral.

In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

If AB, BC and CD are equal chords of a circle with O as centre and AD diameter, than ∠AOB =
From an external point P , tangents PA = PB are drawn to a circle with centre O . If \[\angle PAB = {50}^o\] , then find \[\angle AOB\]
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
Twice the radius is ________________
If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
