Advertisements
Advertisements
प्रश्न
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

उत्तर
It is given that ∠BCD = 100° and ∠ABD = 70°
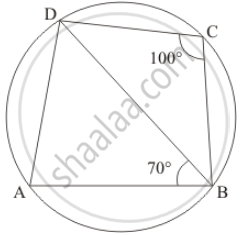
We have to find the ∠ADB
We have
∠A + ∠C = 180° (Opposite pair of angle of cyclic quadrilateral)
So,
`angle A = 180° - 100°`
= 80°
Now in Δ ADB is `angle A ` = 80° and `angle ABD` = 70°
Therefore,
`angle A + angle ADB + angle ABD = 180°`
`80° + angleADB + 70° = 180°`
`angleADB = 180° - 150°`
= 30°
Hence, `angleADB` = 30°
APPEARS IN
संबंधित प्रश्न
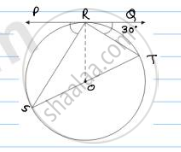
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
In fig. a circle touches all the four sides of quadrilateral ABCD with AB = 6cm, BC = 7cm, CD = 4cm. Find AD.
Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
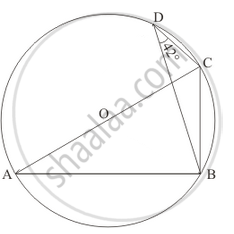
In the given figure, O is the centre of the circle and ∠BDC = 42°. The measure of ∠ACB is
In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

Twice the radius is ________________
Draw any circle and mark
- it's centre
- a radius
- a diameter
- a sector
- a segment
- a point in its interior
- a point in its exterior
- an arc
