Advertisements
Advertisements
प्रश्न
In fig. a circle touches all the four sides of quadrilateral ABCD with AB = 6cm, BC = 7cm, CD = 4cm. Find AD.
उत्तर
We know that the tangents drawn from any external point to circle are equal in length.
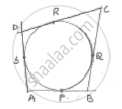
From A ⟶ AS = AP ….(i)
From B ⟶ QB = BP …. (ii)
From C ⟶ QC = RC …..(iii)
From D ⟶ DS = DR …. (iv)
Adding (i), (ii), (iii) & (iv)
(AS + QB + QC + DS) = (AB + BP + RC + OR)
(AS + DS) + (QB + QC) = (AP + BP) + (RC + DR)
AD + BC = AB + CD
⇒ AD + 7 = 6 + 4 AD = 3cm
⇒ AD = 10 – 7 = 3cm
APPEARS IN
संबंधित प्रश्न
From an external point P, tangents PA and PB are drawn to the circle with centre O. If CD is the tangent to the circle at point E and PA = 14 cm. Find the perimeter of ABCD.
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO~Δ ABC.

A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
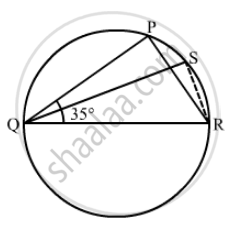
In the given figure, ΔPQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.
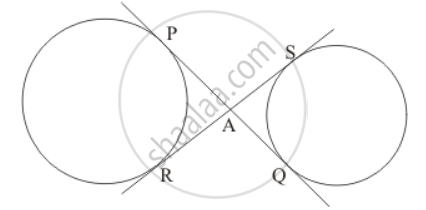
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
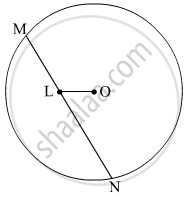
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
Draw a circle of radius 6 cm. In the circle, draw a chord AB = 6 cm.
(i) If O is the center of the circle, join OA and OB.
(ii) Assign a special name to ∆AOB
(iii) Write the measure of angle AOB.
If an isosceles triangle ABC, in which AB = AC = 6 cm, is inscribed in a circle of radius 9 cm, find the area of the triangle.
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.