Advertisements
Advertisements
प्रश्न
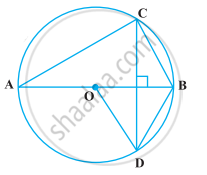
In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.
उत्तर
Given, in the figure BD = OD, CD ⊥ AB.
In ΔOBD, BD = OD ...[Given]
OD = OB ...[Both are the radius of circle]
∴ OB = OD = BD
Thus, ΔODB is an equilateral triangle.
∴ ∠BOD = ∠OBD = ∠ODB = 60°
In ΔMBC and ΔMBD,
MB = MB ...[Common side]
∠CMB = ∠BMD = 90°
And CM = MD ...[In a circle, any perpendicular drawn on a chord also bisects the chord]
∴ ΔMBC ≅ ΔMBD ...[By SAS congruence rule]
∴ ∠MBC = ∠MBD ...[By CPCT]
⇒ ∠MBC = ∠OBD = 60° ...[∵ ∠OBD = 60°]
Since, AB is a diameter of the circle.
∴ ∠ACB = 90°
In ΔACB, ∠CAB + ∠CBA + ∠ACB = 180° ...[By angle sum property of a triangle]
⇒ ∠CAB + 60° + 90° = 180°
⇒ ∠CAB = 180° – (60° + 90°) = 30°
APPEARS IN
संबंधित प्रश्न
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO~Δ ABC.

From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

In the given figure, O is the centre of the two concentric circles of radii 4 cm and 6cm respectively. AP and PB are tangents to the outer and inner circle respectively. If PA = 10cm, find the length of PB up to one place of the decimal.
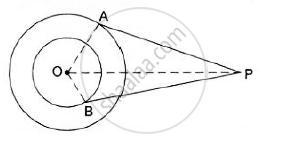
In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

Two circles touch internally. The sum of their areas is 116 π cm2 and the distance between their centres is 6 cm. Find the radii of the circles ?
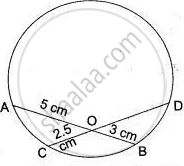
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

The length of tangent from an external point on a circle is always greater than the radius of the circle.
If A, B, C and D are four points such that ∠BAC = 45° and ∠BDC = 45°, then A, B, C, D are concyclic.
From the figure, identify a sector.

