Advertisements
Advertisements
प्रश्न
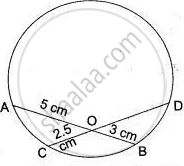
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.
उत्तर
Given:
AO = 5 cm
BO = 3 cm
CO = 2.5 cm
We need to find the length of DO.
From the Intersecting Chords Theorem (or Power of a Point Theorem), we know:
Product of segments of one chord = Product of segments of the other chord
Clearly, chords AB and CD intersect at O.
∴ AO × BO = CO × DO
⇒ 5 × 3 = 2.5 × DO
⇒ DO = `(( 5 xx 3)/2.5)`
= 6 cm.
The length of DO is 6 cm.
APPEARS IN
संबंधित प्रश्न
A chord of a circle of radius 10 em subtends a right angle at its centre. The length of the chord (in em) is
`(A) 5sqrt 2`
`(B) 10 sqrt2`
`(C)5/sqrt2`
`(D) 10sqrt 3`
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
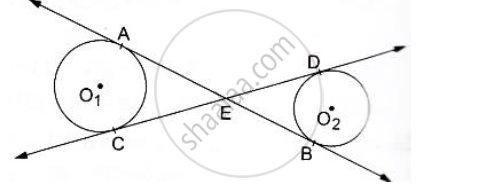
In the given figure common tangents AB and CD to the two circles with centres O1 and O2 intersect at E. Prove that AB=CD
In the given figure, PQ is chord of a circle with centre O an PT is a tangent. If
∠QPT = 60°, find the ∠PRQ.

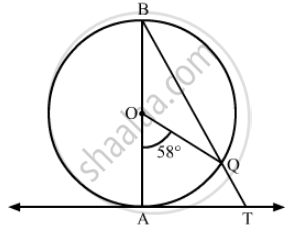
In the given figure, AB is a diameter of a circle with centre O and AT is a tangent. If \[\angle\] AOQ = 58º, find \[\angle\] ATQ.
In the given circle with diameter AB, find the value of x.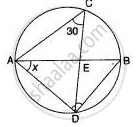
The ______________ is the longest chord of a circle
In the adjoining figure, Δ ABC is circumscribing a circle. Then, the length of BC is ______
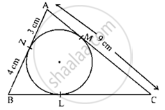
Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of the common chord PQ.
