Advertisements
Advertisements
प्रश्न
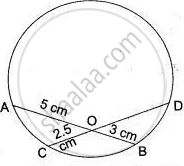
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.
उत्तर
Given:
AO = 5 cm
BO = 3 cm
CO = 2.5 cm
We need to find the length of DO.
From the Intersecting Chords Theorem (or Power of a Point Theorem), we know:
Product of segments of one chord = Product of segments of the other chord
Clearly, chords AB and CD intersect at O.
∴ AO × BO = CO × DO
⇒ 5 × 3 = 2.5 × DO
⇒ DO = `(( 5 xx 3)/2.5)`
= 6 cm.
The length of DO is 6 cm.
APPEARS IN
संबंधित प्रश्न
Two circles touch each other externally at P. AB is a common tangent to the circles touching them at A and B. The value of ∠ L APB is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
In figure OQ : PQ = 3 : 4 and perimeter of ΔPDQ = 60cm. determine PQ, QR and OP.
ture or false v
The degree measure of a semi-circle is 180°.
Prove that two different circles cannot intersect each other at more than two points.
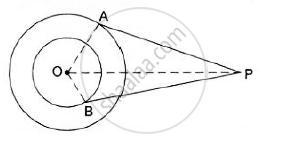
In the given figure, O is the centre of the two concentric circles of radii 4 cm and 6cm respectively. AP and PB are tangents to the outer and inner circle respectively. If PA = 10cm, find the length of PB up to one place of the decimal.
Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.
In an equilateral triangle, prove that the centroid and center of the circum-circle (circumcentre) coincide.
Draw a circle of radius 4.8 cm and mark its center as P.
(i) Draw radii PA and PB such that ∠APB = 45°.
(ii) Shade the major sector of the circle
A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
