Advertisements
Advertisements
प्रश्न
Two circles touch each other externally at P. AB is a common tangent to the circles touching them at A and B. The value of ∠ L APB is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
उत्तर
Correct answer: D
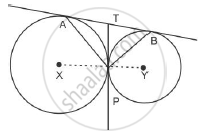
TA = TP ⇒ ∠TAP = ∠TPA
TB = TP ⇒∠TBP = ´TPB
∠TAP + ∠TBP
Correct answer: D

TA = TP ⇒ ∠TAP = ∠TPA
TB = TP ⇒∠TBP = ´TPB
∠TAP + ∠TBP= ∠TPA + ∠TPB= ∠APB
` ∠TAP + ∠TBP+ ∠APB=180^@[because "sum of" ......180^@]`
`/_APB+/_APB=180^@`
`2/_APB=180^@`
`/_APB=90^@`
APPEARS IN
संबंधित प्रश्न
In the given figure, the incircle of ∆ABC touches the sides BC, CA and AB at D, E, F respectively. Prove that AF + BD + CE = AE + CD + BF = `\frac { 1 }{ 2 } ("perimeter of ∆ABC")`
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
In the below fig. O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.

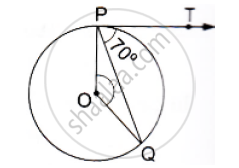
If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.
In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

Use the figure given below to fill in the blank:
Diameter = 2 x ________

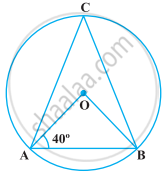
In the following figure, if ∠OAB = 40º, then ∠ACB is equal to ______.
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
