Advertisements
Advertisements
प्रश्न
In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

उत्तर

Given:
OA = 6 cm
OB = 4 cm
AP = 8 cm
Consider ∆OAP.
By Pythagoras' theorem, we have
OA2 + AP2 = PO2
⇒ 62 + 82 = PO2
⇒ PO2 = 100
⇒ PO = 10 cm
Now, consider ∆OBP.
By Pythagoras' theorem, we have
OB2 + BP2 = PO2
⇒ 42 + BP2 = 102
⇒ BP2 = 84
⇒ BP =
Hence, the length of BP is
APPEARS IN
संबंधित प्रश्न
In the given figure, if arc AB = arc CD, then prove that the quadrilateral ABCD is an isosceles– trapezium (O is the centre of the circle).
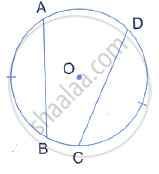
In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
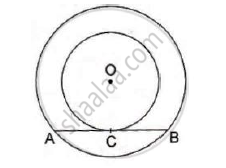
In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB=6cm, BC=9cm and CD=8 cm. Find the length of side AD.
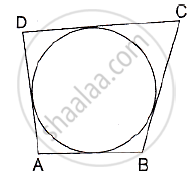
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
A line segment with its end points on the circle is called a ______________
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
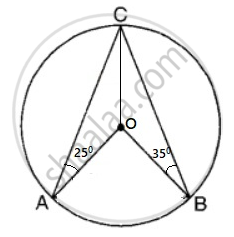
In the adjoining figure ‘O’ is the center of the circle, ∠CAO = 25° and ∠CBO = 35°. What is the value of ∠AOB?
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
