Advertisements
Advertisements
प्रश्न
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
उत्तर
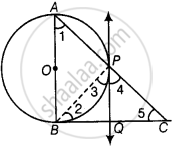
According to the question,
In a right angle ΔABC is which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC at P.
Also PQ is a tangent at P
To Prove: PQ bisects BC i.e. BQ = QC
Proof: ∠APB = 90° ...[Angle in a semicircle is a right-angle]
∠BPC = 90° ...[Linear Pair]
∠3 + ∠4 = 90° ...[1]
Now, ∠ABC = 90°
So in ΔABC
∠ABC + ∠BAC + ∠ACB = 180°
90° + ∠1 + ∠5 = 180°
∠1 + ∠5 = 90° ...[2]
Now, ∠1 = ∠3 ...[Angle between tangent and the chord equals angle made by the chord in alternate segment]
Using this in [2] we have
∠3 + ∠5 = 90° ...[3]
From [1] and [3] we have
∠3 + ∠4 = ∠3 + ∠5
∠4 = ∠5
QC = PQ ...[Sides opposite to equal angles are equal]
But also, PQ = BQ ...[Tangents drawn from an external point to a circle are equal]
So, BQ = QC
i.e. PQ bisects BC.
संबंधित प्रश्न
Two circles touch each other externally at P. AB is a common tangent to the circles touching them at A and B. The value of ∠ L APB is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
In the given figure, AB is a chord of length 16 cm of a circle of radius 10 cm. The tangents at A and B intersect at a point P. Find the length of PA.
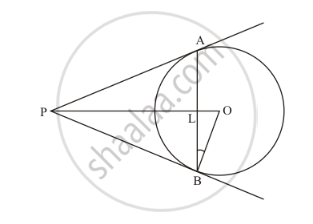
In the given figure, two tangents RQ, and RP and RP are drawn from an external point R to the circle with centre O. If ∠PRQ =120° , then prove that OR = PR + RQ.

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
Use the figure given below to fill in the blank:
Diameter = 2 x ________

If the radius of a circle is 5 cm, what will its diameter be?
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.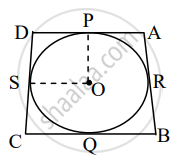
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]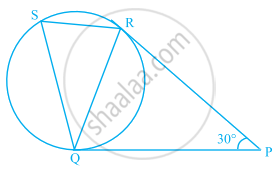
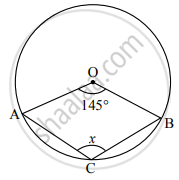
In the given figure, O is the centre of the circle. If ∠ AOB = 145°, then find the value of x.