Advertisements
Advertisements
प्रश्न
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]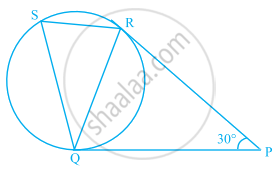
उत्तर
PQ and PR are two tangents drawn from an external point P.
∴ PQ = PR ...[The length of tangents drawn from an external point to a circle are equal]
⇒ ∠PQR = ∠QRP ...[Angles opposite to equal sides are equal]
Now, In ΔPQR,
∠PQR + ∠QRP + ∠RPQ = 180° ...[Sum of all interior angles of any triangle is 180°]
⇒ ∠PQR + ∠PQR + 30° = 180°
⇒ 2∠PQR = 180° – 30° = 150° ...[∵ ∠PQR = ∠QRP]
⇒ ∠PQR = `(180^circ - 30^circ)/2` = 75°
Since, SR || QP
∴ ∠SRQ = ∠RQP = 75° ...[Alternative interior angles]
Also, ∠PQR = ∠QSR = 75° ...[By alternative segment theorem]
In ΔQRS,
∠Q + ∠R + ∠S = 180° ...[Sum of all interior angles of any triangles is 180°]
⇒ ∠Q = 180° – (75° + 75°) = 30°
∴ ∠RQS = 30°
APPEARS IN
संबंधित प्रश्न
Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle, is bisected at the point of contact.
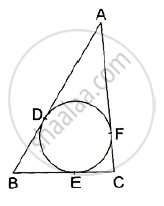
In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14cm, BC = 8cm and CA=12 cm. Find the length AD, BE and CF.
If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
On a semi-circle with AB as diameter, a point C is taken, so that m (∠CAB) = 30°. Find m(∠ACB) and m (∠ABC).
Two concentric circles are of diameters 30 cm and 18 cm. Find the length of the chord of the larger circle which touches the smaller circle.
In a circle with centre P, chord AB is parallel to a tangent and intersects the radius drawn from the point of contact to its midpoint. If AB = `16sqrt(3)`, then find the radius of the circle
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.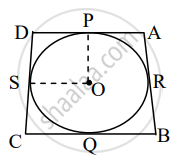
If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is ______.
From the figure, identify the centre of the circle.
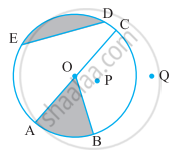
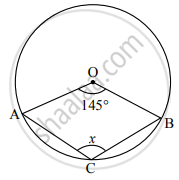
In the given figure, O is the centre of the circle. If ∠ AOB = 145°, then find the value of x.