Advertisements
Advertisements
प्रश्न
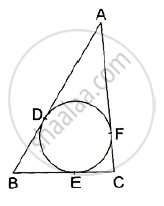
In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14cm, BC = 8cm and CA=12 cm. Find the length AD, BE and CF.
उत्तर
We know that tangent segments to a circle from the same external point are congruent
Now, we nave
AD = AF,BD = BE and CE = CF
Now AD + BD = 14cm …..(1)
AF + FC = 12cm
⇒ AD + FC = 12cm .........(2)
BE + EC = 8cm
⇒ BD + FC= 8 cm ...........(3)
Adding all these we get
AD + BD + AD +FC +BD+ FC = 342
⇒ 2(AD + BD + FC) = 34
⇒ AD+ BO+ FC = 17cm ............(4)
Solving (1) and (4), we get
FC = 3cm
Solving (2) and (4), we get
BD = 5cm = BE
Solving (3) and (4), we get
and AD = 9cm
APPEARS IN
संबंधित प्रश्न
Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). Find the values of y. Hence find the radius of the circle.
In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 60° then find the measure of ∠OAB.

In the given figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

A line segment which joins any two points on a circle is a ___________
All the radii of a circle are _______________
The length of tangent from an external point on a circle is always greater than the radius of the circle.
If an are subtends an angle of 90° at the centre of a circle, then the ratio of its length to the circumference of the circle is ______.
