Advertisements
Advertisements
प्रश्न
Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). Find the values of y. Hence find the radius of the circle.
उत्तर
A and B are the two points that lie on the circle and O is the centre of the circle.
Therefore, OA and OB are the radii of the circle.
Using the distance formula, we have:
`OA=sqrt((-1-2)^2+(y+3y)^2)=sqrt(9+16y^2)`
`OB=sqrt((5-2)^2+(7+3y)^2)=sqrt(9+(7+3y)^2)`
Now, OB = OA (Radii of the same circle)
`sqrt(9+(7+3y)^2)=sqrt(9+16y^2)`
9+(7+3y)2=9+16y^2 (squaring both the sides)
49+9y2+42y=16y2
⇒7y2−42y−49=0
⇒y2−6y−7 =0
⇒y2−7y+y−7=0
⇒(y−7)(y+1)=0
⇒y−7=0 or y+1=0
⇒y=7 or y=−1
When y = 7:
Radius of the circle, `OA=sqrt(9+16y^2)=sqrt(9+16×49)=sqrt(793)`
When y = −1:
Radius of the circle, `OA=sqrt(9+16y^2) =sqrt(9+16×1)=sqrt(25)=5`
APPEARS IN
संबंधित प्रश्न
Write True or False. Give reasons for your answers.
A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
In figure PA and PB are tangents from an external point P to the circle with centre O. LN touches the circle at M. Prove that PL + LM = PN + MN
In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.

In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

Draw a circle of radius 4.8 cm and mark its center as P.
(i) Draw radii PA and PB such that ∠APB = 45°.
(ii) Shade the major sector of the circle
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
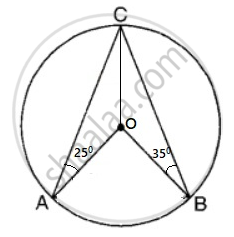
In the adjoining figure ‘O’ is the center of the circle, ∠CAO = 25° and ∠CBO = 35°. What is the value of ∠AOB?
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
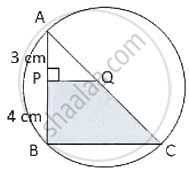
In the adjoining figure, AC is a diameter of the circle. AP = 3 cm and PB = 4 cm and QP ⊥ AB. If the area of ΔAPQ is 18 cm2, then the area of shaded portion QPBC is ______.