Advertisements
Advertisements
Question
Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). Find the values of y. Hence find the radius of the circle.
Solution
A and B are the two points that lie on the circle and O is the centre of the circle.
Therefore, OA and OB are the radii of the circle.
Using the distance formula, we have:
`OA=sqrt((-1-2)^2+(y+3y)^2)=sqrt(9+16y^2)`
`OB=sqrt((5-2)^2+(7+3y)^2)=sqrt(9+(7+3y)^2)`
Now, OB = OA (Radii of the same circle)
`sqrt(9+(7+3y)^2)=sqrt(9+16y^2)`
9+(7+3y)2=9+16y^2 (squaring both the sides)
49+9y2+42y=16y2
⇒7y2−42y−49=0
⇒y2−6y−7 =0
⇒y2−7y+y−7=0
⇒(y−7)(y+1)=0
⇒y−7=0 or y+1=0
⇒y=7 or y=−1
When y = 7:
Radius of the circle, `OA=sqrt(9+16y^2)=sqrt(9+16×49)=sqrt(793)`
When y = −1:
Radius of the circle, `OA=sqrt(9+16y^2) =sqrt(9+16×1)=sqrt(25)=5`
APPEARS IN
RELATED QUESTIONS
true or false
A circle is a plane figure.
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

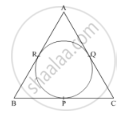
In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
In following fig. ABC is an equilateral triangle . A circle is drawn with centre A so that ot cuts AB and AC at M and N respectively. Prove that BN = CM.

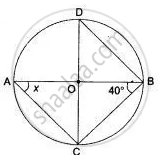
If O is the centre of the circle, find the value of x in each of the following figures
Find the radius of the circle
Diameter = 24 cm
Find the radius of the circle
Diameter = 30 cm
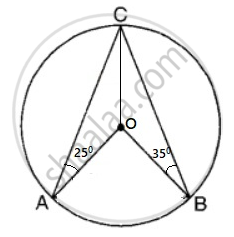
In the adjoining figure ‘O’ is the center of the circle, ∠CAO = 25° and ∠CBO = 35°. What is the value of ∠AOB?
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.