Advertisements
Advertisements
Question
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.
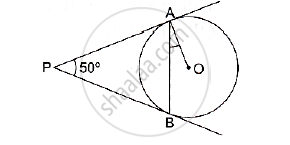
Solution
Construction: Join OB
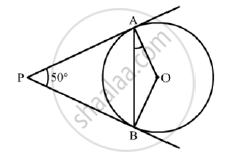
We know that the radius and tangent are perpendicular at their point of contact
∴ ∠OBP = ∠OAP = 90°
Now, In quadrilateral AOBP
∠AOB + ∠OBP + ∠APB + ∠OAP = 360° [Angle sum property of a quadrilateral]
⇒ ∠AOB + 90° + 50° + 90° = 360°
⇒ 230° + ∠BOC= 360°
⇒ ∠AOB = 130°
Now, In isosceles triangle AOB
∠AOB + ∠OAB +∠OBA =180° [Angle sum property of a triangle]
⇒ 130° + 2∠OAB = 180° [∵ ∠OAB = ∠OAB]
⇒ ∠OAB = 25°
APPEARS IN
RELATED QUESTIONS
ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
In fig., O is the centre of the circle, PA and PB are tangent segments. Show that the quadrilateral AOBP is cyclic.
From a point P, two tangents PA and PB are drawn to a circle with center O. If OP =
diameter of the circle shows that ΔAPB is equilateral.
In the following figure, AB is the diameter of a circle with centre O and CD is the chord with length equal to radius OA.
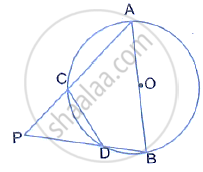
Is AC produced and BD produced meet at point P; show that ∠APB = 60°
If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
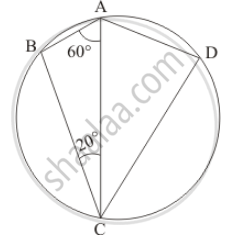
In the given figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
Draw circle with diameter: 6 cm
In above case, measure the length of the radius of the circle drawn.
A line segment which joins any two points on a circle is a ___________
Find the diameter of the circle
Radius = 8 cm
