Advertisements
Advertisements
प्रश्न
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

उत्तर
Construction: Join OB
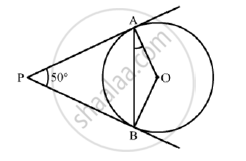
We know that the radius and tangent are perpendicular at their point of contact
∴ ∠OBP = ∠OAP = 90°
Now, In quadrilateral AOBP
∠AOB + ∠OBP + ∠APB + ∠OAP = 360° [Angle sum property of a quadrilateral]
⇒ ∠AOB + 90° + 50° + 90° = 360°
⇒ 230° + ∠BOC= 360°
⇒ ∠AOB = 130°
Now, In isosceles triangle AOB
∠AOB + ∠OAB +∠OBA =180° [Angle sum property of a triangle]
⇒ 130° + 2∠OAB = 180° [∵ ∠OAB = ∠OAB]
⇒ ∠OAB = 25°
APPEARS IN
संबंधित प्रश्न
Prove that the tangents at the extremities of any chord make equal angles with the chord.
In the fig. a circle is inscribed in a quadrilateral ABCD in which ∠B = 90° if AD = 23cm,
AB = 29cm and DS = 5cm, find the radius of the circle.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
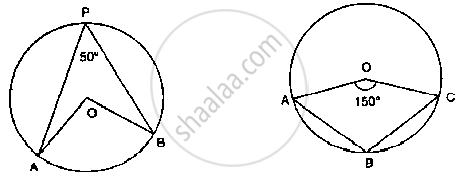
In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
In the given figure, O is the centre of the circle. Find ∠CBD.

In the given figure, a ∆ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the lengths of sides AB and AC, when area of ∆ABC is 84 cm2.

In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
A line segment which joins any two points on a circle is a ___________
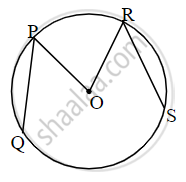
In figure, O is the centre of a circle, chord PQ ≅ chord RS. If ∠POR = 70° and (arc RS) = 80°, find
(i) m(arc PR)
(ii) m(arc QS)
(iii) m(arc QSR)
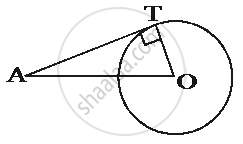
A point A is 26 cm away from the centre of a circle and the length of the tangent drawn from A to the circle is 24 cm. Find the radius of the circle.