Advertisements
Advertisements
प्रश्न
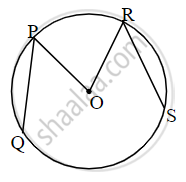
In figure, O is the centre of a circle, chord PQ ≅ chord RS. If ∠POR = 70° and (arc RS) = 80°, find
(i) m(arc PR)
(ii) m(arc QS)
(iii) m(arc QSR)
उत्तर
(i) m(arc PR) = m∠POR ...[Definition of measure of arc]
∴ m(arc PR) = 70°
(ii)
chord PQ ≅ chord RS .....[Given]
∴ m(arc PQ) = m(arc RS) = 80° .....[Corresponding arcs of congruent chords of a circle are congruent]
Now,
m(arc QS) + m(arc PQ) + m(arc PR) + m(arc RS) = 360° ...[Measure of a circle is 360°]
∴ m(arc QS) + 80° + 70° + 80° = 360°
∴ m(arc QS) + 230° = 360°
∴ m(arc QS) = 130°
(iii) m(arc QSR) = m(arc QS) + m(arc SR) = 130° + 80° ...[Arc addition property]
m(arc QSR) = 210°
APPEARS IN
संबंधित प्रश्न
n Fig. 2, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then ∠QOR equals:
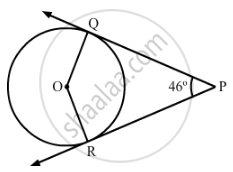
(A) 67°
(B) 134°
(C) 44°
(D) 46°
Write True or False. Give reason for your answer.
A circle is a plane figure.
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
In the below fig. O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

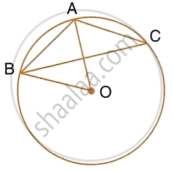
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
- ∠AOB,
- ∠ACB,
- ∠ABC.
The perimeter (in cm) of a square circumscribing a circle of radius a cm, is
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

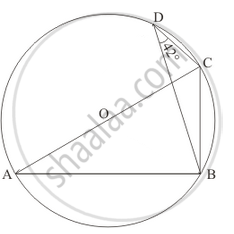
In the given figure, O is the centre of the circle and ∠BDC = 42°. The measure of ∠ACB is
Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius `4sqrt(2)` cm and also find ∠OAC and ∠OCA
Find the radius of the circle
Diameter = 30 cm
In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
In the figure, O is the centre of a circle, AB is a chord, and AT is the tangent at A. If ∠AOB = 100°, then ∠BAT is equal to ______

In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at point A, then ∠BAT is equal to ______.
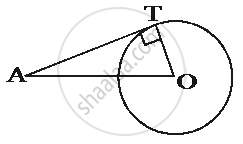
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
A point A is 26 cm away from the centre of a circle and the length of the tangent drawn from A to the circle is 24 cm. Find the radius of the circle.
Draw any circle and mark
- it's centre
- a radius
- a diameter
- a sector
- a segment
- a point in its interior
- a point in its exterior
- an arc
Find the length of the arc of a circle which subtends an angle of 60° at the centre of the circle of radius 42 cm.
Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius of a circle.
