Question

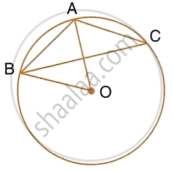
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:

1. ∠AOB, 
2. ∠ACB,
3. ∠ABC.

Answer 1

i. Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.

∴ `∠ACB = 1/2∠AOB`

Since AB is the side of a regular hexagon,

∠AOB = 60°

ii. `∠AOB = 60^circ => ∠ACB = 1/2 xx 60^circ = 30^circ`

iii. Since AC is the side of a regular octagon,

`∠AOC = 360^circ/8 = 45^circ`

Again, Arc AC subtends ∠AOC at the center and ∠ABC at the remaining part of the circle.

`=> ∠ABC = 1/2 ∠AOC`

`=> ∠ABC = 45^circ/2 = 22.5^circ`