Advertisements
Advertisements
प्रश्न
If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
विकल्प
True
False
उत्तर
This statement is False.
Explanation:
Consider the given figure.
In which we have a circle with centre O and AB a chord with ∠AOB = 60°
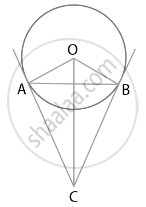
Since, tangent to any point on the circle is perpendicular to the radius through point of contact,
We get,
OA ⊥ AC and OB ⊥ CB
∠OBC = ∠OAC = 90° ...[Equation (1)]
Using angle sum property of quadrilateral in Quadrilateral AOBC,
We get,
∠OBC + ∠OAC + ∠AOB + ∠ACB = 360°
90° + 90° + 60° + ∠ACB = 360°
∠ACB = 120°
Hence, the angle between two tangents is 120°.
APPEARS IN
संबंधित प्रश्न
ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
Find the length of a tangent drawn to a circle with radius 5cm, from a point 13 cm from the center of the circle.
In the fig. ABC is right triangle right angled at B such that BC = 6cm and AB = 8cm. Find the radius of its in circle.
AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
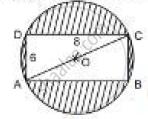
Find the area of the shaded region in the figure If ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle. (Take π= 3.14)
The center of a circle is at point O and its radius is 8 cm. State the position of a point P (point P may lie inside the circle, on the circumference of the circle, or outside the circle), when:
(a) OP = 10.6 cm
(b) OP = 6.8 cm
(c) OP = 8 cm
Twice the radius is ________________
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
Is every diameter of a circle also a chord?
