Advertisements
Advertisements
प्रश्न
AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
उत्तर
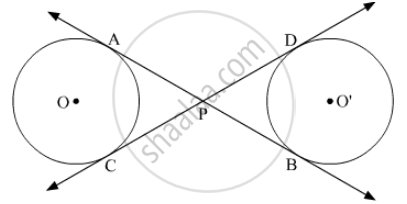
Given: Two circles with centre’s O and O'. AB and CD are common tangents to the circles which intersect in P.
To Prove: AB = CD
Proof:
AP = PC (length of tangents drawn from an external point to the circle are equal) ..… (1)
PB = PD (length of tangents drawn from an external point to the circle are equal) ..… (2)
Adding (1) and (2), we get
AP + PB = PC + PD
⇒ AB = CD
Hence Proved
APPEARS IN
संबंधित प्रश्न
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
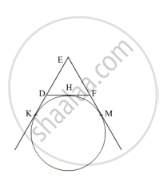
In Fig 2, a circle touches the side DF of ΔEDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, then the perimeter of ΔEDF (in cm) is:
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
An equilateral triangle ABC is inscribed in a circle with centre O. The measures of ∠BOCis
In the given figure, if ∠ABC = 45°, then ∠AOC =
In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
A point A is 26 cm away from the centre of a circle and the length of the tangent drawn from A to the circle is 24 cm. Find the radius of the circle.
The circumcentre of a triangle is the point which is ______.
