Advertisements
Advertisements
प्रश्न
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.
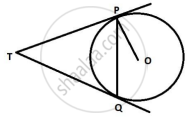
उत्तर १
Given: A circle with centre O and an external point T from which tangents TP and TQ are drawn to touch the circle at P and Q.
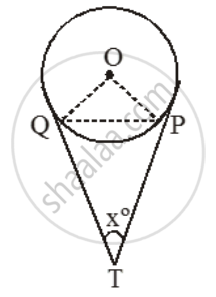
To prove: ∠PTQ = 2∠OPQ.
Proof: Let ∠PTQ = xº. Then,
∠TQP + ∠TPQ + ∠PTQ = 180º
[∵ sum of the ∠s of a triangle is 180º]
⇒ ∠TQP + ∠TPQ = (180º – x) ….(i)
We know that the lengths of tangent drawn from an external point to a circle are equal.
So, TP = TQ.
Now, TP = TQ
⇒ ∠TQP = ∠TPQ
`=\frac{1}{2}(180^{0}-x)=( 90^\text{o}-\frac{x}{2})`
∴ ∠OPQ = (∠OPT–∠TPQ)
`=90^{0}-( 90^\text{o}-\frac{x}{2})=\frac{x}{2} `
`⇒ ∠OPQ = \frac { 1 }{ 2 } ∠PTQ`
⇒ 2∠OPQ = ∠PTQ
उत्तर २
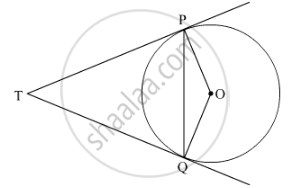
Given: TP and TQ are two tangents of a circle with centre O and P and Q are points of contact
To prove: ∠PTQ = 2∠OPQ
Suppose ∠PTQ = θ.
Now by theorem, "The lengths of a tangents drawn from an external point to a circle are equal".
So, TPQ is an isoceles triangle.
Therefore, ∠TPQ = ∠TQP = `1/2`(180°− θ) = 90°−`θ/2`.
Also by theorem "The tangents at any point of a circle is perpendicular to the radius through the point of contact" ∠OPT = 90°.
Therefore,
∠OPQ = ∠OPT − ∠TPQ
`= 90^@ - (90^@ - 1/2theta)`
`= 1/2 theta`
= `1/2` ∠PTQ
Hence, 2∠OPQ = ∠PTQ.
APPEARS IN
संबंधित प्रश्न
In Fig. 8, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.

Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm; find the length of another chord.
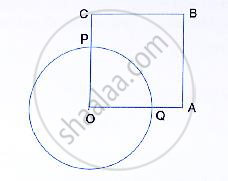
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC
at P and OA at Q. Prove that:
(i) ΔOPA ≅ ΔOQC, (ii) ΔBPC ≅ ΔBQA.
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.

In the given figure, O is the centre of the circle. PA and PB are tangents. Show that AOBP is cyclic quadrilateral.

Two circles touch internally. The sum of their areas is 116 π cm2 and the distance between their centres is 6 cm. Find the radii of the circles ?
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF

C(O, r1) and C(O, r2) are two concentric circles with r1 > r2 AB is a chord of C(O, r1) touching C(O, r2) at C then ______
If a chord AB subtends an angle of 60° at the centre of a circle, then the angle between the tangents at A and B is ______
AB is a chord of a circle with centre O. AOC is diameter of circle, AT is a tangent at A.
Write answers of the following questions:
- Draw the figure using the given information.
- Find the measures of ∠CAT and ∠ABC with reasons.
- Whether ∠CAT and ∠ABC are congruent? Justify your answer.
