Advertisements
Advertisements
प्रश्न
Two circles touch internally. The sum of their areas is 116 π cm2 and the distance between their centres is 6 cm. Find the radii of the circles ?
उत्तर
Let r1 be the radius of the bigger circle and r2 be the radius of the smaller circle.
It is given that the two circles touch each other internally.
∴ Difference between their radii = Distance between the centres of the two circles
⇒ r1 − r2 = 6 cm .....(1)
Also,
Sum of their areas = 116π cm2
\[\therefore \pi {r_1}^2 + \pi {r_2}^2 = 116\pi\]
\[ \Rightarrow {r_1}^2 + {r_2}^2 = 116 . . . . . \left( 2 \right)\]
From (1) and (2), we have
\[\left( r_2 + 6 \right)^2 + {r_2}^2 = 116\]
\[ \Rightarrow {r_2}^2 + 12 r_2 + 36 + {r_2}^2 = 116\]
\[ \Rightarrow 2 {r_2}^2 + 12 r_2 - 80 = 0\]
\[ \Rightarrow {r_2}^2 + 6 r_2 - 40 = 0\]
\[ \Rightarrow {r_2}^2 + 10 r_2 - 4 r_2 - 40 = 0\]
\[ \Rightarrow r_2 \left( r_2 + 10 \right) - 4\left( r_2 + 10 \right) = 0\]
\[ \Rightarrow \left( r_2 + 10 \right)\left( r_2 - 4 \right) = 0\]
\[ \Rightarrow r_2 + 10 = 0 or r_2 - 4 = 0\]
\[ \Rightarrow r_2 = - 10 or r_2 = 4\]
Since the radius of a circle cannot be negative, so r2 = 4 cm.
∴ r1 = r2 + 6 = 4 + 6 = 10 cm
Thus, the radii of the circles are 4 cm and 10 cm.
APPEARS IN
संबंधित प्रश्न
Two circles touch each other externally at P. AB is a common tangent to the circles touching them at A and B. The value of ∠ L APB is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
Two circles touch externally at a point P. from a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and E respectively. Prove that TQ = TR.
Fill in the blank
A continuous piece of a circle is ............... of the circle
true or false
A chord of a circle, which is twice as long is its radius is a diameter of the circle.
If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
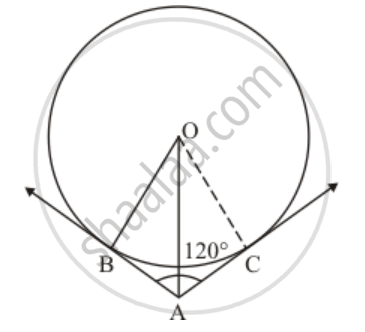
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
Use the figure given below to fill in the blank:
AB is a ______ of the circle.

Construct a triangle PQR in which, PQ = QR = RP = 5.7 cm. Draw the incircle of the triangle and measure its radius.
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
