Advertisements
Advertisements
प्रश्न
Two circles touch internally. The sum of their areas is 116 π cm2 and the distance between their centres is 6 cm. Find the radii of the circles ?
उत्तर
Let r1 be the radius of the bigger circle and r2 be the radius of the smaller circle.
It is given that the two circles touch each other internally.
∴ Difference between their radii = Distance between the centres of the two circles
⇒ r1 − r2 = 6 cm .....(1)
Also,
Sum of their areas = 116π cm2
\[\therefore \pi {r_1}^2 + \pi {r_2}^2 = 116\pi\]
\[ \Rightarrow {r_1}^2 + {r_2}^2 = 116 . . . . . \left( 2 \right)\]
From (1) and (2), we have
\[\left( r_2 + 6 \right)^2 + {r_2}^2 = 116\]
\[ \Rightarrow {r_2}^2 + 12 r_2 + 36 + {r_2}^2 = 116\]
\[ \Rightarrow 2 {r_2}^2 + 12 r_2 - 80 = 0\]
\[ \Rightarrow {r_2}^2 + 6 r_2 - 40 = 0\]
\[ \Rightarrow {r_2}^2 + 10 r_2 - 4 r_2 - 40 = 0\]
\[ \Rightarrow r_2 \left( r_2 + 10 \right) - 4\left( r_2 + 10 \right) = 0\]
\[ \Rightarrow \left( r_2 + 10 \right)\left( r_2 - 4 \right) = 0\]
\[ \Rightarrow r_2 + 10 = 0 or r_2 - 4 = 0\]
\[ \Rightarrow r_2 = - 10 or r_2 = 4\]
Since the radius of a circle cannot be negative, so r2 = 4 cm.
∴ r1 = r2 + 6 = 4 + 6 = 10 cm
Thus, the radii of the circles are 4 cm and 10 cm.
APPEARS IN
संबंधित प्रश्न
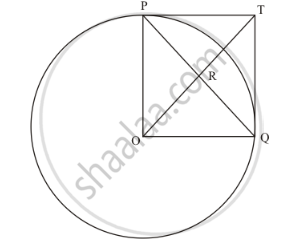
In the given figure, PO⊥QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OT are right bisector of each other.
In the following figure, AB is the diameter of a circle with centre O and CD is the chord with length equal to radius OA.
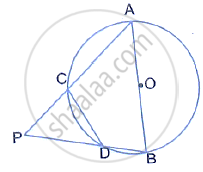
Is AC produced and BD produced meet at point P; show that ∠APB = 60°
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

In the given figure, two tangents RQ, and RP and RP are drawn from an external point R to the circle with centre O. If ∠PRQ =120° , then prove that OR = PR + RQ.
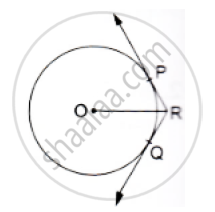
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 60° then find the measure of ∠OAB.

A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
Twice the radius is ________________
In the adjoining figure, seg DE is the chord of the circle with center C. seg CF⊥ seg DE and DE = 16 cm, then find the length of DF?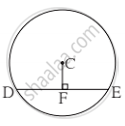
C(O, r1) and C(O, r2) are two concentric circles with r1 > r2 AB is a chord of C(O, r1) touching C(O, r2) at C then ______
AB is a chord of a circle with centre O. AOC is diameter of circle, AT is a tangent at A.
Write answers of the following questions:
- Draw the figure using the given information.
- Find the measures of ∠CAT and ∠ABC with reasons.
- Whether ∠CAT and ∠ABC are congruent? Justify your answer.
